Curvas que separan: fácil de entender, difícil de demostrar
Hablamos sobre un intuitivo resultado sobre curvas cuya demostración es sorprendentemente compleja

En lo que se refiere a enunciados y demostraciones, el mundo de los teoremas matemáticos es de lo más variado. Los hay con enunciados cortitos y enunciados largos, y los podemos encontrar con formulaciones muy claras y sencillas de explicar y con formulaciones bastante complejas. Y en lo que se refiere a las demostraciones, hay de todo: bellas, farragosas, cortitas, insufriblemente largas, geométricas, analíticas…Lo que decíamos, de todo.
El caso es que en matemáticas todo resultado propuesto se tiene que demostrar para que se considere correcto. Pero es cierto que algunos teoremas son tan claros e intuitivos que parece que no necesitan demostración para afirmar su veracidad. Hoy vamos a hablar de, posiblemente, el caso más claro y representativo de este tipo de resultados: el teorema de la curva de Jordan. El enunciado de este teorema es de lo más simple, intuitivo y sencillo de explicar y comprender, pero, por contra, las demostraciones que se conocen de él son largas, complejas y técnicas o necesitan de utilizar alguna teoría muy avanzada.
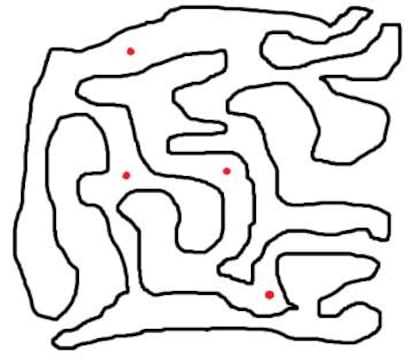
Antes de enunciar este teorema, vamos a introducir el problema poco a poco. Toma papel y boli y dibuja una curva cerrada y que no se corte a sí misma. Sí, la que quieras, puede ser muy sencillita, como una circunferencia, o más “compleja”, como la que veis en la imagen. Está más o menos claro que dicha curva deja una porción del papel “dentro” de la misma y otra porción “fuera” de la misma, y que esas dos porciones no tienen nada en común, ¿verdad? Y que el borde de ambas porciones es la propia curva que habéis dibujado, ¿verdad? Bien, pues ése es el teorema de la curva de Jordan.
Antes de seguir, vamos a fijarnos en los puntos que hay marcados en la imagen. ¿Sabrías decir cuáles de ellos están “dentro” de la curva y cuáles están “fuera” de la curva? En este caso la cosa es sencilla de ver, pero quizás no sería tan sencillo si la curva fuera mucho más larga, estuviera dibujada en un papel a mayor tamaño y tuviera muchos más giros y complicaciones. La pregunta es, entonces, la siguiente: ¿sabrías dar algún procedimiento que nos asegure, sin ningún género de duda, si un punto está “dentro” o “fuera” de la curva? Responderemos más adelante.
Al parecer, el primero que formuló este resultado fue el matemático francés Camille Jordan a finales del siglo XIX. El propio Jordan presentó una demostración del mismo, pero resultó ser incorrecta. El primero que dio una demostración correcta de este teorema fueOswald Veblen en 1905. El teorema de la curva de Jordan puede enunciarse de manera informal (en el sentido de que me voy a ahorrar algunos detalles técnicos) como sigue:
Toda curva cerrada representada en un plano que no se corte a sí misma divide el plano en dos regiones sin puntos comunes: la “interior” (acotada) y la “exterior” (no acotada). Además, el borde de ambas regiones es la propia curva.
Planteádselo a cualquier persona, tenga formación matemática o no. Estoy seguro de que lo entenderá sin mucho esfuerzo y, además, lo verá absolutamente evidente. De hecho, es posible que alguien que entienda que los teoremas hay que demostrarlos piense que en este caso ni siquiera haría falta, que la cosa es tan tan evidente que no podría no ser cierta. O, en el caso de asumir que hay que demostrarlo, pensaría que la demostración debe ser bastante sencilla…
…pues no es así: las demostraciones que se conocen de este teorema son realmente complicadas. Algunas son muy largas y muy técnicas, y otras más cortas lo son porque usan teorías muy potentes y avanzadas, por lo que en realidad también son muy complicadas y técnicas. De éstas últimas no vamos a comentar nada más, pero de las primeras sí.
La demostración larga y técnica de la que tengo conocimiento usa como idea inicial el tema que os planteaba antes como ejercicio. ¿Cómo saber si un punto está “dentro” de una curva o “fuera” de la misma? Pues hay un procedimiento relativamente simple para verlo: cortes transversales.
Una recta corta transversalmente a una curva si dicha no es tangente a la curva en ese punto de corte. En la siguiente imagen podéis ver un corte transversal y uno que no lo es:
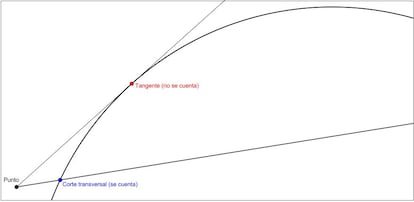
Bien, pues podemos utilizar esto para determinar si un punto está en el interior o en el exterior de la curva. Desde el punto, trazamos una semirrecta hacia una zona que sepamos con seguridad que está en el exterior de la curva y contamos cuántos cortes transversales hay (si hay alguno tangente no lo contamos). Si el número de cortes transversales es par, el punto estaba en el exterior de la curva, y si es impar entonces el punto estaba en el interior de la curva. Os animo a que probéis este sencillo método en la imagen anterior o en la curva que vosotros mismos habéis dibujado antes.
Pues ésta es la clave de la demostración que os comentaba. La idea es definir dos conjuntos:
A={puntos para los cuales toda semirrecta trazada desde ellos corta transversalmente a la curva un número impar de veces}
B={puntos para los cuales toda semirrecta trazada desde ellos corta transversalmente a la curva un número par de veces}
Y demostrar (y aquí está lo verdaderamente complicado) que en ambos conjuntos hay puntos, que no tienen puntos comunes y que su unión nos da el plano completo excepto la propia curva inicial. Parece fácil, pero os aseguro que no lo es.
Y ahora la pregunta es natural: ¿qué ocurre en otras dimensiones? Pues para curvas hay una generalización a cualquier dimensión denominada teorema de separación de Jordan-Brouwer, pero para superficies la cosa falla, por ejemplo, en tres dimensiones (ahora mismo no tengo conocimiento sobre lo que ocurre en dimensiones mayores). Para quien esté interesado, aquí tenéis un artículo que escribí hace un tiempo sobre un contraejemplo en tres dimensiones: la esfera cornuda de Alexander.
Como comenté unos párrafos más arriba, es cierto que me he saltado mucho detalles técnicos, tanto en las definiciones como, evidentemente, en la demostración. Este resultado es cierto para toda curva que pueda deformarse, sin romperla, hasta una circunferencia (estas curvas se denominan curvas de Jordan), pero entre ellas hay casos extraños que son difíciles de analizar: curvas con picos, puntos desde los cuales se pueden trazar semirrectas que cortan transversalmente a la curva infinitas veces (por lo que habla de par o impar no tiene sentido) y algunas otras situaciones complicadas de estudiar. Posiblemente todo esto sea lo que provoque que las demostraciones sean tan engorrosas: no debe ser fácil pasar por encima de tanto caso patológico…
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































