La resolución de la cúbica: una historia llena de historias

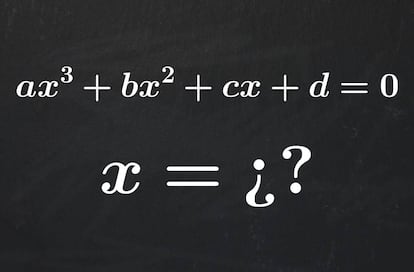
Unos de los temas relacionados con matemáticas que se tratan durante nuestra vida académica es el de la resolución de ecuaciones. Aprendemos a resolver muchos tipos (exponenciales, logarítmicas, racionales, trigonométricas…), pero analizando los métodos de resolución podemos concluir que muchas de ellas se reducen a resolver una ecuación polinómica. Por tanto, los métodos de resolución de estas ecuaciones polinómicas tienen una gran importancia dentro de esta parte de nuestra formación matemática.

Para resolver estas ecuaciones polinómicas, lo primero que se tiene en cuenta es el grado de dicha ecuación. Las ecuaciones de grado 1 son sencillas de resolver (operar, separar términos y despejar), y para las de grado 2 tenemos una fórmula que prácticamente todos los que hemos pasado por el instituto solemos recordar: menos b más menos raíz cuadrada de… ¿Os acordáis? Es ésta:

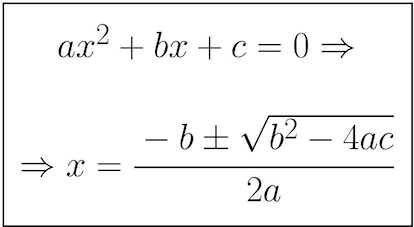
¿Qué ocurre con las de grado 3 y superior? Pues aquí la cosa se vuelve algo difusa: algunas se resuelven mediante factorización, también podemos buscar soluciones con Ruffini (muy mítica la regla de Ruffini), en algunos casos podemos ayudarnos de cambios de variable convenientes (como en las bicuadradas y similares)… Pero el caso es que cuando el grado es mayor o igual que 3 nadie nos da una fórmula tipo la que tenemos para grado 2 que nos dé las soluciones (si existen) en todos los casos.

¿Existen dichas fórmulas para grados superiores a dos? Pues sí…para grado 3 y grado 4. Y hoy vamos a hablar de la historia que rodea a la fórmula de resolución de la de grado 3: hoy hablamos sobre la resolución de la cúbica.

Nuestra historia se sitúa en el siglo XVI y tiene como protagonistas principales a Niccolo Fontana (apodado Tartaglia por ser tartamudo), Girolamo Cardano, Scipione del Ferro y Ludovico Ferrari y como actores secundarios a Antonio Maria del Fiore y Annibale della Nave. Sobre la década de los 30 de este siglo, llega a oídos de Tartaglia que un tal del Fiore posee un método para resolver ecuaciones cúbicas. En una época como aquella, en la que el interés por el álgebra estaba creciendo de manera significativa entre los matemáticos en Europa, poseer un método para resolver estas ecuaciones resultaba valiosísimo. Por ello, espoleado por la posibilidad de que dicho método pudiera existir, Tartaglia se puso a trabajar en el tema, encontrando tal método por sí mismo (al menos eso parece) un tiempo después.

En aquella época, era habitual organizar desafíos entre matemáticos en los que cada uno proponía problemas que el otro tenía que resolver. Pues a raíz del trabajo de Tartaglia, se organizó uno que lo enfrentaba a del Fiore, resultando Tartaglia ganador de manera aplastante (resolvió todos los problemas propuestos por del Fiore, mientras que este no fue capaz de resolver ninguno de los que le tocaron).

Cuando Cardano tuvo conocimiento de esta aplastante victoria de Tartaglia, intenta convencerlo para que le revele el método que había descubierto y así poder publicarlo en su obra Ars Magna, que estaba preparando en aquellos años. Aunque Tartaglia se niega en primera instancia, al final le revela su descubrimiento con la condición de que no lo publique (aunque, al parecer, Cardano estaba dispuesto a otorgarle a Tartaglia en su obra la autoría del descubrimiento).

Lo que Tartaglia había descubierto eran métodos para resolver las ecuaciones cúbicas que no tienen término de grado dos. Aunque en la actualidad todas ellas se reducen a una única forma, en aquella época se expresaban de estas tres maneras, x³+px=q, x³=px+q y x³+q=px, y cada una tenía su propio método de resolución (los números negativos todavía no se aceptaban con demasiada naturalidad). A partir de estos métodos, Cardano y su ayudante Ludovico Ferrari consiguen un método para resolver la cúbica general x³+mx²+nx=r. Esta ecuación puede reducirse fácilmente a una del tipo x³+px=q, por lo que solamente haría falta resolver ésta. Sus soluciones vienen dadas por la siguiente expresión:

Aunque parece que solamente tenemos un valor, en realidad esta expresión representa los tres valores de las tres soluciones de la cúbica general. Sin entrar en demasiados detalles, lo más interesante de ellos, y tremendamente novedoso en aquella época, es que en ocasiones dos de las soluciones contenían raíces cuadradas de números negativos, dando lugar a lo que hoy conocemos como números complejos.

Y aquí viene la clave de la historia: del Fiore conocía el método de resolución porque Scipione del Ferro, profesor suyo, se lo había comunicado años antes. Es decir, del Ferro fue el primero (que se sepa) que creó un método de resolución para una cúbica. En 1542, Cardano y Ferrari viajan a Bolonia en busca de los trabajos de del Ferro, y es Della Nave (yerno de del Ferro) quien se los proporciona.

Al verlos, Cardano comprueba que el método de del Ferro para resolver la cúbica x³+px=q era el mismo que el de Tartaglia, por lo que entiende que la promesa que le había hecho este de no publicar su descubrimiento ya no tiene validez. Cardano publica el método de del Ferro en Ars Magna en 1545, y Tartaglia entra en cólera. Aunque Cardano lo nombra varias veces en su obra, Tartaglia se siente traicionado…

…y responde publicando un año después un libro con su método y con ataques a Cardano. Este no responde a dichos ataques, pero sí lo hace Ferrari. Este enfrentamiento acaba con un nuevo “duelo matemático” entre Tartaglia y Ferrari que se convierte en un auténtico fenómeno social. Durante el duelo se produce una discusión por uno de los problemas, lo que lleva a aplazarlo al día siguiente. Pero Tartaglia, al parecer por el apoyo de la multitud a Ferrari, no se presenta, por lo que Ludovico es declarado ganador.

Y podemos decir que, básicamente, aquí acaba todo. Como todas las historias, esta todavía plantea algunos interrogantes que, posiblemente, nunca podamos resolver. Por ejemplo, poseer un método de resolución de la cúbica proporcionaba mucha ventaja en los duelos entre matemáticos, en los que en ocasiones se podían conseguir jugosas recompensas. Se entiende que del Ferro le comunicara a della Nave su descubrimiento (era su yerno), pero lo que no se sabe es por qué también se lo comunicó a del Fiore. Y otra pregunta sin respuesta es si Tartaglia de verdad desarrolló él mismo su método o “se inspiró” en trabajos anteriores, atribuyéndose después la autoría. Como decía, es posible que nunca tengamos respuesta a estas y otras preguntas.

Para terminar, es interesante comentar que en Ars Magna también se publicó un método para resolver las ecuaciones de grado cuatro. Dicho método, desarrollado por Ferrari, consiste en reducir (de una manera muy inteligente) la ecuación de grado cuatro a una cúbica, y después resolver dicha cúbica. Con ello cerramos también el círculo con las ecuaciones de grado cuatro.

¿Qué ocurre con las de grado 5 y superior? Pues que no hay fórmula general para resolverlas. Todo lo relacionado con este descubrimiento es también muy interesante y merece la pena contarlo, pero eso será ya otro día.