Una igualdad rebosante de belleza

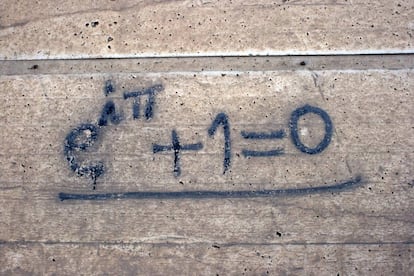
Al igual que en otras disciplinas, como la literatura, el arte o la música, dentro de las matemáticas también podemos encontrar belleza, mucha belleza. La geometría es, posiblemente, una de las ramas donde se pueden encontrar resultados más bellos (como, por ejemplo, el de la circunferencia de Feuerbach), pero también podemos encontrar bellezas matemáticas jugando con números (los cuadrados mágicos habituales y los menos habituales son buenos ejemplos de ello).

Pero estoy convencido de que la igualdad que os traigo hoy es, para muchos, el culmen de la belleza matemática. Me refiero, cómo no, a la identidad de Euler:

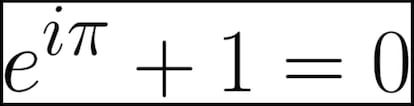
Ni ecuación (no hay en ella ninguna incógnita) ni fórmula (no hay ninguna relación entre magnitudes): igualdad o identidad de Euler. La identidad de Euler es una igualdad que relaciona de una manera preciosa cinco de los números más importantes y representativos de las matemáticas: 0, 1, e, i y π. Y hoy vamos a explicar cómo se llegó a esa maravillosa relación.

La identidad de Euler es un caso particular de la conocida como fórmula de Euler (no confundir con la fórmula de Euler para poliedros), aunque Roger Cotes ya publicó algo relacionado con ella antes que Euler (aunque no escrita de la forma habitual). La fórmula en cuestión aparece en Introductio in analysin infinitorum, posiblemente la obra más conocida e importante del gran Leonhard Euler. En la página 104 del Volumen I de la misma podemos ver cómo un desarrollo anterior culmina en la siguiente expresión:

Tomando v como un ángulo, y sabiendo que en la actualidad a √-1 se representa con la letra i, tenemos la que ahora conocemos como fórmula de Euler:

Aunque en este blog nos dedicamos a la divulgación matemática a nivel general, no queremos renunciar a los desarrollos matemáticos. Por ello, a continuación presentamos una demostración de dicha fórmula.

Partimos de la expresión de e^x como serie de potencias:

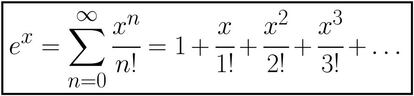
En ella, sustituimos x por iz. Usando que i¹=i, i²=-1, i³=-I y que i⁴=1 (y que el ciclo se repite de ahí en adelante), y separando después los términos de exponente par por un lado y los de exponente impar por otro tenemos lo siguiente:

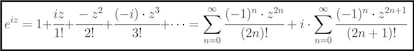
Y da la maravillosa casualidad de que los desarrollos en serie de cos(z) y sen(z) son exactamente esas dos últimas series (y en ese orden). Por tanto, ya tenemos la esperada y buscada fórmula de Euler:

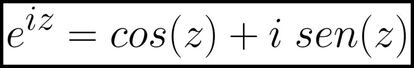
La identidad de Euler, protagonista de este artículo, sale de la fórmula de Euler al sustituir z por π, sabiendo que cos(π)=-1 y sen(π)=0 y sumando 1 a ambos lados de la ecuación:

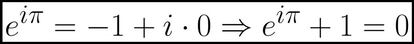
La tremenda belleza que rodea a esta identidad hace que aparezca de manera recurrente en muchos lugares. Es magnífica para aparecer en obras de arte, y los grafitis dan una buena prueba de ello. Hay muchos que tienen a la identidad de Euler como protagonista, y concretamente en Granada podemos encontrar unos cuantos. En la imagen tenéis un par de ejemplos. A la izquierda tenéis una que se puede ver en la calle Gonzalo Gallas, saliendo por la puerta trasera de la Facultad de Ciencias (muchísimas gracias a Antonio Bueno por acercarte a hacer la foto y por enviármela). Y a la derecha tenéis otra en la pared de una casa en el campo que encuentra en alguna de las salidas que hay en la autovía Jaen-Granada:

Tengo que agradecer a Modesto, el autor de la foto, que se haya preocupado por buscarla y mandármela. Espero que pararas para hacerla, ya que admirar tanta belleza matemática en una sola expresión podría provocar un accidente.

Por cierto, en Pintando Granada podéis ver otro grafiti de la identidad de Euler que puede contemplarse en esta maravillosa ciudad.

También podemos encontrarla en esa maravillosa serie de humor que lleva retratando a la sociedad americana (bueno, y a la mundial) desde hace muchos muchos años: Los Simpson. El frikismo científico es una característica común a gran parte de sus guionistas (Manuel Ansede nos habló de ello, centrado en las matemáticas, en Los diez mejores momentos matemáticos de ‘Los Simpson’), y ello ha propiciado que esta identidad aparezca en varios capítulos. Aquí tenéis algunas imágenes de los mismos:

Y, cómo no, es también perfecta para modificaciones corporales. Es habitual verla en tatuajes, como éste que Eva me envió hace tiempo:

o en éste del gran Eugenio, autor del blog Ciencia en el XXI:

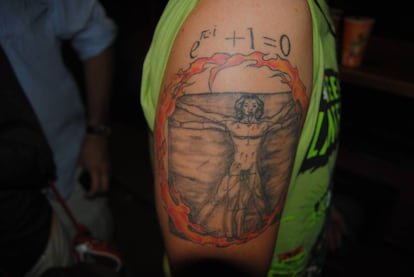
Y también es protagonista es escarificaciones, como puede verse en esta impactante imagen:

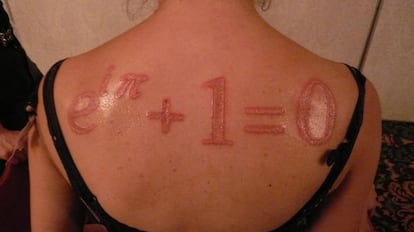
Seguro que vosotros conocéis otros lugares en los que aparece. Os agradeceremos muchos que compartáis vuestras experiencias y vuestras imágenes en los comentarios.