El grafo adivinador de la letra del DNI

En más de una ocasión he hablado con gente sobre si saben cómo se asigna la letra del DNI, y en la mayoría de los casos he recibido la misma respuesta: no lo sé. Casi todos me acaban diciendo que piensan que podría ser una asignación al azar, aunque en ocasiones (pocas) me he encontrado con gente que cree que debe haber una especie de fórmula que se encargue de esta tarea. La realidad es que son estos últimos quienes están en lo cierto. En el presente artículo vamos a hablar sobre cómo se hace este cálculo de la letra del DNI y también explicaremos cómo construir un grafo adivinador de la letra del DNI.

Vamos a comenzar explicando cuál es el método de asignación de letra al número del DNI, que, dicho sea de paso, es bastante sencillo. Tomamos el número del DNI, de 8 cifras, lo dividimos entre 23 y nos quedamos con el resto de dicha división. Después buscamos ese resto en la siguiente tabla y tomamos la letra que le corresponda:

Si queréis, podéis comprobarlo con vuestro propio DNI. ¿Que no tenéis ganas de dividir entre 23? Usad calculadora… Ups, pero la calculadora, normalmente, no muestra el resto de la división, ¿verdad? No hay problema: dividís vuestro número de DNI entre 23, le quitáis los decimales al resultado, multiplicáis lo que os quede por 23 y le restáis lo que os dé a vuestro número de DNI, y ya tenéis el resto. Veamos un ejemplo con el número 34567890:

34567890/23 = 1502951’7391…

1502951 · 23 = 34567873

34567890 – 34567873 = 17

Miramos en la tabla anterior y vemos que, como el resto es 17, al número 34567890 le corresponde la letra V.

Visto esto, vamos a construir nuestro grafo adivinador. Para quien no lo sepa, un grafo es básicamente un conjunto de puntos (que tiene al menos uno), que se llaman vértices, y un conjuntos de líneas (podría no haber ninguna, aunque en ese caso el grafo tendría poco interés) que conectan parejas de puntos, llamadas aristas. En nuestro caso, construiremos un grafo dirigido, lo que significa que las aristas serán flechas que se pueden recorrer en un solo sentido.

Nuestro “grafo adivinador” va a tener 23 vértices. En principio, en ellos colocamos los 23 posibles restos que se pueden obtener al dividir entre 23, de 0 a 22. Disponemos estos vértices en círculo en el orden que indica la propia tabla, y unimos cada uno con el siguiente con una flecha (son las flechas negras de la imagen siguiente) hasta cerrar el círculo.

Ahora dibujamos un nuevo grupo de flechas (las rojas de la imagen posterior) según la siguiente regla: cada vértice V se une con una flecha con el resto que queda al dividir 10 · V entre 23. Por ejemplo, para ver con cuál habrá que unir el vértice 7 hacemos 10 · 7 = 70 y dividimos 70 entre 23. Esa división da resto 1, por lo que del 7 saldrá una flecha que llegará al 1. Y, por poner otro ejemplo, para el 11 tenemos que 10 · 11 es 110, y la división de 110 entre 23 da de resto 18, por lo que del 11 saldrá una flecha que llegará al 18.

Cuando tengamos todas esas flechas dibujadas, sustituimos cada resto, los números del 0 al 22 que pusimos al principio, por la letra que le corresponde en la tabla anterior, y nos queda nuestro grafo adivinador de la letra del DNI:

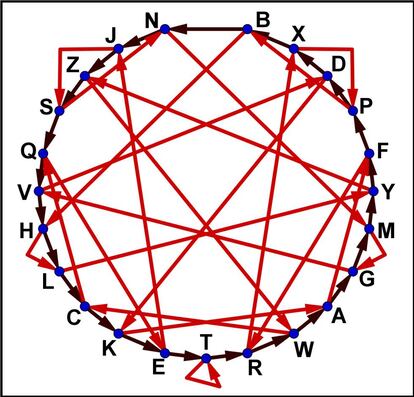
Bonito, ¿verdad? Veamos ahora cómo podemos usarlo para adivinar la letra de un DNI español. La cosa es como sigue:

Comenzando en la T, tomamos el primer dígito del DNI y recorremos tantas flechas negras como diga ese dígito. Cuando lleguemos a una letra, recorremos la flecha roja que sale de ella. Desde ahí, hacemos lo mismo con el segundo dígito, las flechas negras que diga y luego la roja. Así hasta el séptimo dígito. Después recorremos las negras que diga el octavo dígito, y la letra en la que terminemos es la letra que hay que asignar al número inicial.

Veamos como ejemplo cuál nos quedaría para el número que usamos unos párrafos más arriba, el 34567890:

T – 3 negras – A – Roja – F

F – 4 negras – B – Roja – H

H – 5 negras – T – Roja – T

T – 6 negras – Y – Roja – Z

Z – 7 negras – K – Roja – A

A – 8 negras – B – Roja – H

H – 9 negras – G – Roja – V

V – 0 negras – V -----> Nuestra letra es la V, tal y como habíamos visto anteriormente.

Veamos otro ejemplo con el número de DNI que coincide con la fecha de hoy, 25012017. La secuencia de letras sería la siguiente:

T – W – C – W – C – C – Q – V – D – B – H – H – L – C – Q – T

Curiosamente, 25012017 es múltiplo de 23, por lo que su resto al dividirlo entre 23 es 0. Por tanto, tal y como nos ha dicho nuestro grafo adivinador de letra del DNI, la letra que le corresponde al número 25012017 es la T.

Lo que hemos construido es el grafo de divisibilidad del 23, con el que podemos calcular el resto que deja un número cualquiera al dividirlo entre 23 siguiendo la regla de las flechas que hemos descrito. Pero esto se puede hacer para cualquier número m mayor que 1:

Colocamos los números de 0 hasta m – 1 en círculo y los unimos en orden con flechas (las negras) hasta cerrar el círculo. Después, cada vértice k se une con el resto que se obtiene al dividir 10 · k entre m (las flechas rojas).

Aunque es evidente, creo que es interesante comentar que estos grafos pueden usarse como "criterios de divisibilidad" entre m: si para un número obtenemos resto 0, entonces dicho número es múltiplo de m.

Os animo a que creéis alguno y a que comprobéis que funciona. Y dicho esto pregunto: ¿por qué funciona este método? A ver quién nos lo explica en los comentarios.