¿Por qué las antenas parabólicas son parabólicas?

En ocasiones, los estudios y trabajos matemáticos se consideran innecesarios, prescindibles o una pérdida de tiempo aludiendo, principalmente, falta de utilidad o nulas aplicaciones prácticas de los mismos. Hoy, en este artículo, os traigo un caso que ejemplifica que estos estudios son necesarios, aunque en un principio no se les vea aplicación práctica, ya que nunca se sabe cuándo ni dónde podremos encontrarles utilidad: las antenas parabólicas. Su forma no alude a una cuestión estética ni a un capricho de algún fabricante, sino que responde a una cuestión meramente matemática, que concretamente usa de forma muy inteligente una propiedad de las parábolas conocida desde hace casi 2000 años.

Antes de nada, vamos a recordar qué son las parábolas. Una parábola es una cónica (curva que surge de hacer un cierto corte a un cono) que se define como el conjunto de puntos que están a la misma distancia de un punto concreto, llamado foco, y una cierta recta, llamada directriz. En la siguiente imagen podéis ver una parábola (en rojo), su foco y su directriz y la igualdad de distancias a esos dos objetos desde varios puntos de la misma:

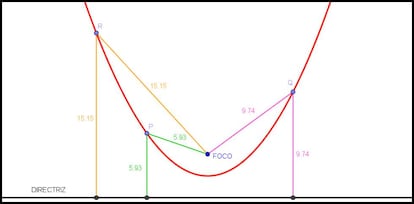
A partir de esta definición, es fácil construir un objeto en 3D girando la parábola respecto de un eje vertical que pasa por su foco. Al hacer esto, obtenemos una superficie tridimensional denominada paraboloide:

¿Os suena? Exacto, acabamos de crear una antena parabólica, cuyo foco es el mismo que el de la parábola que hemos girado.

¿Por qué esta forma es útil? Pues por una interesante propiedad de las parábolas que describimos a continuación:

Un punto del interior de la parábola que se mueva por una recta paralela al eje “rebotará” en la parábola y será enviado hacia el foco.

Esto significa que si mandamos señales hacia la parábola que sean paralelas al eje, éstas serán reflejadas por ella hacia el foco, independientemente de la recta que usemos. Aquí tenéis una demostración de este hecho, atribuida a Dositeo. Tenéis una muestra gráfica en este applet de GeoGebra. Y en este otro applet podéis verlo de forma animada.

Y esto es muy útil, ya que con un paraboloide que tenga un receptor de señal colocado en el foco podemos conseguir que todas las señales que reboten en el paraboloide acaben siendo enviadas a dicho receptor, sin necesidad de tener que apuntar directamente al mismo. Es decir, con un pequeño receptor obtenemos una gran recepción de señal utilizando toda la superficie del paraboloide de la forma descrita.

Esta propiedad no se utiliza solamente para las antenas parabólicas, sino para otros dispositivos, como cocinas solares. Se construye un paraboloide que refleje los rayos del sol y se coloca en su foco el objeto a cocinar, consiguiendo así que se caliente mucho más rápido. Esto también puede usarse para acumular energía solar, colocando un acumulador en el foco del paraboloide.

Por otra parte, esta propiedad también se puede usar de manera inversa. Colocamos en el foco del paraboloide un emisor de señal orientado hacia el paraboloide y emitimos dicha señal hacia la mayor parte posible de su superficie. Todas las señales “rebotarán” en la misma y se reflejará de forma paralela a su eje hacia afuera, consiguiendo así mayor emisión de señal que la que obtendríamos emitiendo solamente desde un punto. Por ejemplo, esto se puede usar en faros de vehículos (colocando una bombilla en el foco para emitir mayor cantidad de luz) o en micrófonos parabólicos (con un micrófono en el foco mara emitir sonido a mayor superficie).

Y para finalizar, otra curiosidad. Como podéis ver en la imagen principal que ilustra este artículo, el foco del paraboloide está sujeto con cuatro barras rectas que se apoyan en la superficie del mismo (hay que sujetarlo de alguna forma). Esto tiene el problema de que algunas señales, tanto si emitimos como si recibimos, pueden rebotar en estas barras y, por tanto, perderse. Para evitar esto, lo que se hace en algunas ocasiones es tomar para la antena una parte del paraboloide que no esté “debajo” del foco, sino “a un lado”, como puede verse también en las dos antenas que aparecen a la derecha en la imagen principal, o en la que podéis ver a la derecha. Así evitamos esos rebotes en las sujeciones, y conseguimos una antena más eficiente.

Como podéis ver, estudios que en un principio se hacen sin pensar en posibles usos acaban encontrando aplicaciones prácticas muy interesantes y útiles, que, en este caso, han supuesto un gran desarrollo en muchos campos. Por ello, sería ideal que no subestimemos los estudios matemáticos, por muy abstractos que nos parezcan. Nunca se sabe cuándo pueden sernos de ayuda en el día a día.

¿Conocéis más aparatos que utilicen esta interesante propiedad de las parábolas en su funcionamiento? Contádnoslo en los comentarios.