El sobre mágico de Lewis Carroll

EL PAÍS y Materia proponen a sus lectores, cada semana, un juego de lógica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta será ofrecida en la columna de la semana siguiente.

Podemos estar seguros de que Kant ni siquiera intentó pasar una y solo una vez por los siete puentes de Königsberg, pues Leonhard Euler ya había demostrado (en 1736, cuando Kant tenía doce años) que tal recorrido era imposible.

Para resolver el problema, Euler empezó por reducir el plano de Königsberg a un esquema en el que cada una de las cuatro zonas de la ciudad (dos islas fluviales y ambas márgenes del río Pregel) es representada por un punto y cada puente por una línea que conecta dos de esos puntos.

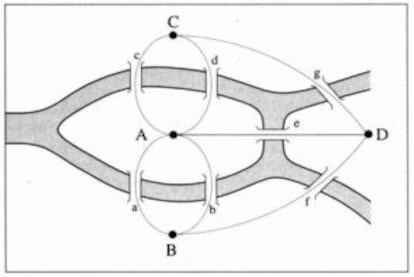
Luego Euler vio que en los puntos intermedios del recorrido tenían que confluir un número par de líneas, pues por cada tramo de llegada tenía que haber uno de salida; solo en el punto inicial y en el punto final del recorrido debían confluir un número impar de líneas (con la posibilidad, claro está, de que el punto inicial y el final fueran el mismo). Pero, como se puede ver en el diagrama, en todos los puntos confluyen un número impar de líneas (3, 3, 3 y 5 respectivamente), por lo que el recorrido es imposible.

Euler no se limitó a resolver el problema de los puentes, sino que lo generalizó en un trabajo que tituló Solutio problematis ad geometriam situs pertinentis, que se considera el punto de partida de la teoría de grafos, e incluso de la topología.

Un grafo es un conjunto de puntos (denominados nodos o vértices) unidos por unas líneas o aristas que representan algún tipo de conexión entre ellos. La forma y el tamaño de las aristas es irrelevante, por lo que un grafo no es una estructura geométrica sino topológica. Pues la topología no se ocupa de las formas y los tamaños concretos de las figuras, sino de propiedades más generales, como la continuidad, la proximidad, la compacidad o, como en este caso, la conectividad.

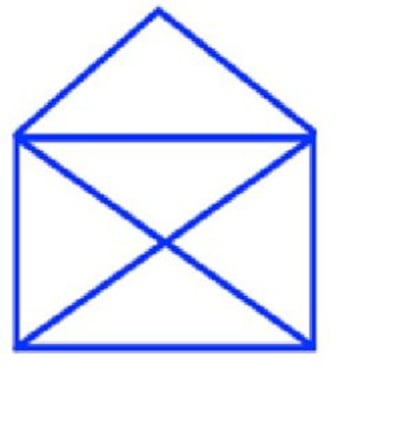
Hay numerosos acertijos lógicos directamente relacionados con los recorridos exhaustivos, como los que consisten en dibujar una figura sin levantar el lápiz del papel ni pasar dos veces por un mismo trazo. Uno de los más conocidos consiste en dibujar de un solo trazo un sobre abierto como el de la figura que se muestra, en azul, en el párrafo anterior.

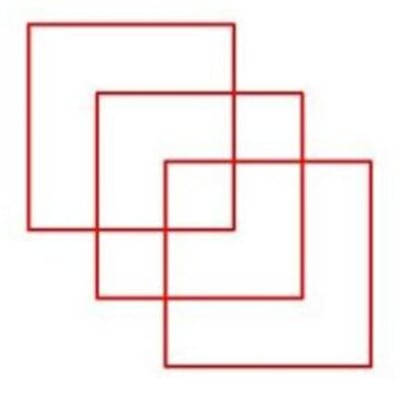
Algo más difícil de dibujar de un solo trazo es la figura que Lewis Carroll le envió por carta en 1869 a una de sus jóvenes amigas, como se muestra, en rojo, en la fugura de la izquierda...

Carlo Frabetti

Escritor y matemático, miembro de la Academia de Ciencias de Nueva York, ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’