Un reloj de dos colores
Elisa Lorenzo García, estudiante de doctorado de la Universidad Politécnica de Cataluña, plantea el cuarto desafío matemático de EL PAÍS. Durante 30 semanas publicaremos un problema en coordinación con la Real Sociedad Matemática Española, que en 2011 cumple 100 años. El plazo para enviar soluciones a este problema ya está cerrado. Hoy daremos la solución y sortearemos entre los acertantes la biblioteca matemática que ofrece EL PAÍS cada domingo. Esta semana, Los números primos, de Enrique Gracián, por 9,95 euros con el periódico.
Nota: Para evitar confusiones y permitir también la participación de los lectores sordos, incluimos aquí el enunciado del problema por escrito.
Se considera un reloj con sus 12 números en torno a una circunferencia: 1, 2, ..., 12. Se pintan de azul o rojo cada uno de los 12 números de modo que haya seis pintados de azul y seis de rojo. El problema consiste en demostrar, que, independientemente del orden en que se hayan pintado, siempre existirá una posible recta que divida al reloj por la mitad, dejando en cada lado seis números, tres pintados de rojo y tres pintados de azul.
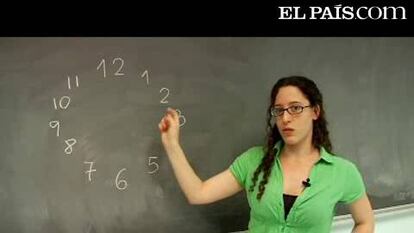
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































