Las encuestas igualan las fuerzas de ERC y Ciudadanos en Cataluña

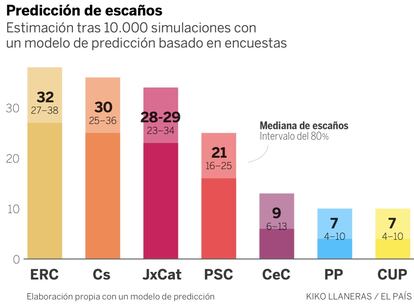
Quedan siete días para las elecciones catalanas y las encuestas no han parado de moverse. Esta es la predicción actualizada de nuestro modelo estadístico. El modelo agrega docenas de sondeos (publicados antes del 13 de diciembre) y ha sido calibrado con la precisión histórica de miles de encuestas y doscientas elecciones.

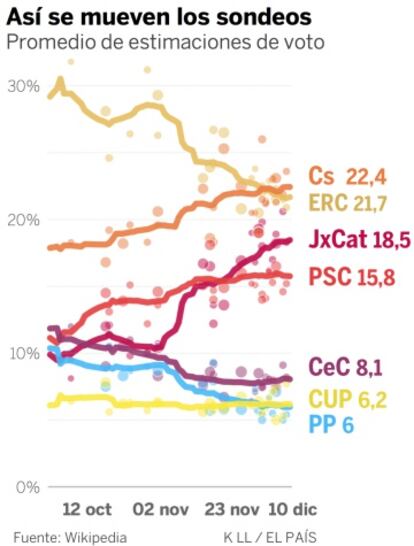
Esta semana los sondeos han igualado a Ciudadanos con ERC. El promedio coloca a Ciudadanos unas décimas por delante, con el 22,4% de los votos. Le siguen ERC (21,7%), Junts per Catalunya (18,5%), PSC (15,8%), CeC-Podem (8,1%), la CUP (6,2%) y el PP (6%). La tendencia más firme es un trasvase de votos desde ERC a JxCat, que lleva produciéndose semanas y no se detiene.

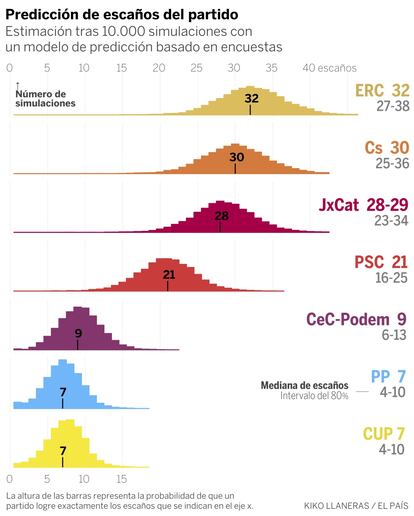
Tomando el promedio de votos, nuestro modelo predice los escaños que logrará cada partido. Para eso hacemos 10.000 simulaciones de las elecciones en cada provincia, tal y como se explica en la metodología. El gráfico a continuación representa el resultado de cada partido.

El modelo estima que ERC rondará los 32 escaños, y que le siguen Ciudadanos (30), JxCat (28-29), PSC (21), CeC-Podem (9), PP (7) y la CUP (7). El gráfico también hace visible la incertidumbre de estas elecciones. Los intervalos al 80% de probabilidad son horquillas de unos diez escaños, que pueden parecer demasiado grandes, pero no son caprichosas: vienen determinadas por el acierto histórico de miles de encuestas. ERC puede moverse entre los 27 y los 38 diputados, Ciudadanos entre 25 y 36, y JxCat entre 23 y 34. El orden de los partidos no está en absoluto decidido.

En el 53% de las simulaciones, ERC es la fuerza con más escaños. Ciudadanos es primero en un 29%, y JxCat, en el 18%. La carrera se ha igualado en los últimos días. Hace una semana la probabilidad de ganar en escaños era del 75% para ERC, del 17% para Cs, y del 7% para JxCat. Por eso es importante pensar en las tendencias: si uno está seguro de que ERC va a seguir perdiendo terreno respecto Cs y JxCat, debe igualar aún más sus opciones de victoria.

La pregunta clave: las posibles mayorías

La batalla por el primer puesto es importante, pero la pregunta fundamental del 21 de diciembre es sobre coaliciones: ¿qué probabilidades tienen distintos partidos de sumar 68 diputados y poder escoger el próximo gobierno? Esa es una predicción que no pueden hacer las encuestas convencionales, pero que ofrece nuestro modelo electoral.

El gráfico representa la suma de escaños para distintos partidos en 10.000 simulaciones del 21D. La masa a la derecha de los 68 escaños representa la probabilidad de que alcancen la mayoría.

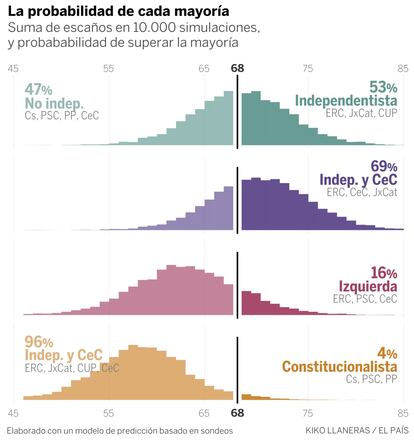
Ahora mismo, nuestra predicción es que los independentistas (ERC, JxCat y la CUP) tienen un 53% de probabilidades de conseguir una mayoría de escaños. Sus opciones equivalen prácticamente a lanzar una moneda al aire. En el 47% restante de las veces, en cambio, son Cs, PSC, PP y CeC quienes suman 68 escaños y podrían buscar un acuerdo de gobierno.

El modelo ve difícil que los tres partidos del bloque constitucionalista logren una mayoría solos. La suma de Cs, PSC y PP ronda los 58 escaños. No es imposible que mejoren sus encuestas hasta alcanzar los 68, pero solo pasa 4 de cada 100 veces. Sus opciones mejoran si los independentistas no tienen mayoría, pero ni siquiera con esa condición superan el 10% de probabilidad.

Los sondeos de esta semana también hacen improbable un pacto entre ERC, los comunes y el PSC. El acuerdo es complicado política y aritméticamente: la suma de los tres partidos sólo alcanza los 68 escaños en el 16% de las simulaciones. La fuga de votos de ERC hacía JxCat, y la caída de los comunes en los sondeos, ha alejado esta posibilidad.

Una tercera alternativa al bloque independentista es que ERC gobierne apoyado por JxCat y los comunes. Estos tres partidos suman 68 escaños el 69% de las veces. Es probable, pero en absoluto seguro (la probabilidad de que no sumen es más o menos la misma que la de ver fallarse un tiro libre en baloncesto). Además en este caso es importante un matiz. la probabilidad de esta suma se reduce si el bloque independentista no suma. Si ERC, JxCat y la CUP se quedan por debajo de 68 diputados, las probabilidades de que sumen JxCat, ERC y los comunes caen al 46%.

En los próximos días se publicarán las últimas encuestas, que servirán para que sepamos si las tendencias se han parado o si JxCat y Ciudadanos siguen subiendo. Con todas esas encuestas publicaremos la última actualización de nuestro modelo e incluiremos predicciones de votos, escaños, provincias y posibles mayorías.

Metodología de nuestro modelo. Las predicciones las produce un modelo estadístico basado en sondeos y en su precisión histórica. El modelo es similar al que usamos en Francia y Reino Unido. Funciona en cuatro pasos: 1) agregar y promediar las encuestas en Cataluña, 2) proyectar ese promedio sobre cada provincia, 3) incorporar la incertidumbre esperada, y 4) simular 10.000 elecciones para calcular probabilidades.

Paso 1. Promediar las encuestas. El modelo agrega las estimaciones de voto de docenas de sondeos. La mayoría pueden consultarse en Wikipedia. Hay dos razones para hacer este promedio: sirve para reducir el error de muestreo y además ofrece una «cocina» de consenso. El promedio está ponderado para tener en cuenta el tamaño de muestra, la empresa encuestadora y la fecha del sondeo. También penalizo las encuestas de una misma empresa en fechas cercanas, para evitar que dominen excesivamente la media. El promedio está ponderado por fecha según una ley exponencial decreciente (con una vida medida de 7 días y una ventana que ignora las encuestas con más de 14 días).

Paso 2. Proyectar el promedio a cada provincia. Antes de calcular los escaños es necesario estimar el porcentaje de votos de cada partido en cada provincia. Para eso hacemos una proyección lineal del promedio de votos en todo Cataluña. La proyección tiene en cuenta resultados históricos en cada provincia (del 26J y el 27S) y los últimos sondeos del CIS y del CEO.

Paso 3. Incorporar la incertidumbre de las encuestas. Este paso es el más complicado. También es el más importante. Para predecir el resultado «más probable» basta usar el promedio de votos y estimar los escaños. Pero si queremos saber qué probabilidad tienen distintos resultados necesitamos algo más: un modelo probabilístico. Necesitamos estimar la precisión esperada para los sondeos en Cataluña. ¿De qué magnitud son los errores habituales? ¿Cómo de probable es que se produzcan errores de 1, 2 o 5 puntos? Para responder esas preguntas hemos analizado el error de miles de encuestas.

Calibrar los errores esperados. Primero he estimado el error de las encuestas en España. He construido una base de datos con encuestas de 23 elecciones desde 1982 —incluyendo todas las generales y una docena de elecciones recientes. El error absoluto medio (MAE) de los promedios de encuestas en España ha rondado los 2,1 puntos por partido. Pero esos errores dependen al menos de dos cosas: del tamaño del partido y de la cercanía de las elecciones. Para tener en cuenta esos dos factores hemos recurrido a la base de datos de Jennings y Christopher Wlezien. Hemos analizado los errores de más de 2.700 encuestas en 198 elecciones de 19 países occidentales. Así hemos construido un modelo sencillo que estima el error MAE del promedio de votos estimado por las encuestas para cada partido, teniendo en cuenta: i) su tamaño (es más fácil estimar un partido que ronda el 5% en votos que uno que supera el 30%), y ii) los días que faltan hasta las elecciones (porque las encuestas mejoran al final).

Paso 4. Simular. El último paso consiste en ejecutar el modelo 10.000 veces. Cada iteración es una simulación de las elecciones con porcentajes de voto que varían según las distribuciones definidas en el paso anterior. Los resultados en esas simulaciones permiten calcular las probabilidades de que haya una mayoría de ciertos partidos, de que un candidato logre cierto número de votos, quede primero, etc.

Por qué encuestas. El modelo se basa por entero en encuestas. Existe la percepción de que los sondeos no son fiables, pero lo cierto es que a nivel nacional fallaron por pocos puntos incluso con Trump y con el Brexit. En otras elecciones recientes, como las francesas, las holandesas o las de País Vasco y Galicia, los sondeos dieron poco que hablar porque estuvieron acertados. Las encuestas raramente son perfectas, pero son capaces de predecir elecciones en términos probabilísticas. Además,no existe una alternativa que haya demostrado mayor capacidad de predicción.