El mayor número primo conocido

Es posible que el número 1398269 no os diga nada especial, pero la realidad es que podemos decir que representa el comienzo de una nueva era dentro de la búsqueda de números primos. Era noviembre de 1996 y se encontraba un número primo de 420921 cifras que a la postre resultó ser especial, y no solamente por la enorme cantidad de dígitos que posee. Pero antes de hablar de ese momento, centremos históricamente el asunto.

La búsqueda de números primos, sobre todo desde que Euclides demuestra que existen infinitos, ha sido un tema que ha apasionado a muchísimos, y muy buenos, matemáticos a lo largo de la historia. Más concretamente, la búsqueda de una fórmula que genere siempre números primos distintos ha quitado el sueño a, posiblemente, todos los matemáticos que se han acercado en sus estudios a este tema.

Una de las épocas en las que esta búsqueda tuvo uno de sus momentos álgidos fue el siglo XVII. La correspondencia de Pierre de Fermat con otros matemáticos marca el comienzo de la teoría de números como rama de las matemáticas, y los números primos son unos de sus principales protagonistas. Fermat da una fórmula que, según dice, genera siempre números primos (todos ellos distintos), pero se equivoca, como demostró Euler más adelante.

Fermat no fue el único. En esa misma época, Marín Mersenne, un sacerdote, matemático y filósofo francés, introduce una expresión aparentemente simple que a la larga ha resultado interesantísima en lo que se refiere a encontrar números primos realmente grandes.

Mersenne estudia los números de la forma 2ⁿ-1 en su obra Cogitata Physica-Mathematica, de 1644, y da algunos datos sobre ellos. Mersenne sabe que esos números, que suelen llamarse M_n, no son siempre primos, pero la sensación es que esta fórmula acaba dando números primos para una cantidad nada despreciable de valores de n. Además, Mersenne da una lista de números primos calculados con esa fórmula hasta n=257. Es cierto que se equivoca (da alguno como primo y omite otros que sí lo son), pero todo este estudio es el comienzo de la búsqueda de números primos de Mersenne.

Los siete primeros números primos de Mersenne, que eran los que se conocían hasta la época del propio Mersene, son los que aparecen en la siguiente tabla:

De aquí en adelante esta lista fue aumentando, pero a un ritmo algo lento. En 1771, Leonhard Euler encuentra el octavo primo de Mersenne, que corresponde con el exponente n=31:

M₃₁ = 2³¹ – 1 = 2147483647

Exceptuando los de exponente muy pequeño, que eran fáciles de comprobar por dar resultados bastante bajos, los primos de Mersenne conocidos hasta ese momento se habían calculado mediante comprobación directa: se probaba un número primo en el exponente, se calculaba el número y después se realizaban divisiones entre los números primos inferiores a él para ver si era divisible entre alguno de ellos. Este método puede ser útil cuando el número a comprobar es relativamente bajo, pero cuando ese número es grande el tiempo dedicado a la comprobación sería tan grande que el método pasa a ser inútil en la práctica.

Por cierto, acabamos de decir que se probaba con números primos en el exponente. ¿Por qué no se probaba con número compuestos? Por ejemplo, ¿no podríamos probar con n=16 ó n=28? Pues sí, podríamos, pero sería totalmente inútil porque se sabe que, si n es compuesto, el número 2ⁿ – 1 también es compuesto (y, por tanto, no es primo). ¿Alguien sabría demostrarlo? Podéis hacerlo en los comentarios.

La búsqueda de números primos de Mersenne avanzó con los estudios de Édouard Lucas, que desarrolló un método para comprobar si un número de la forma 2^p – 1 era primo (mucho más eficaz que el de comprobación directa). Con este método, Lucas demostró, a finales del siglo XIX, que 2¹²⁷ – 1 es un número primo. Hasta mediados de los años 50 del siglo XX, éste era el mayor número primo conocido, y además es el número primo más grande que se ha encontrado sin ayuda de ordenadores.

Y aquí está la clave del asunto: el ordenador. El desarrollo de la informática y el método de Lucas, que fue mejorado por Derrick Henry Lehmer sobre 1930, son los causantes de que hayamos conseguido encontrar números primos de Mersenne muchos más grandes.

Este método, llamado actualmente test de Lucas-Lehmer, consiste en lo siguiente. Supongamos que queremos comprobar si cierto número M_p = 2^p – 1 es primo. Pues, para ello, seguimos el siguiente proceso:

(Podéis ver una demostración de este resultado en este enlace de The Prime Pages, web en la que podéis encontrar gran cantidad de información sobre números primos.)

Aunque s_p-2 es un número mayor que M_p, el test da el resultado mucho más rápido que si hacemos la comprobación directa (por ejemplo, para utilizar este método no necesitamos conocer todos los números primos menores que el número que estamos comprobando).

Sin usar este test, se conocían los 12 primeros números de Mersenne. En 1952 se comienza a utilizar el test de Lucas-Lehmer en un ordenador…y en ese año se encuentran cinco más (del 13 al 17 de la lista). A partir de aquí, la lista continúa creciendo hasta el que ocupa el número 34 en la lista de primos de Mersenne, que ya tiene la nada despreciable cantidad de 378632 dígitos…

…y llegamos al año 1996 que citábamos al principio del artículo. A principios de ese año, George Woltman crea GIMPS (Great Internet Mersenne Prime Search). La idea de esta iniciativa es ofrecer un software, que utiliza el test de Lucas-Lehmer, para que quien quiera pueda descargarlo y así contribuya a la búsqueda de primos de Mersenne. Cuando se encuentra un número de la forma 2^p – 1 que el test da como primo, se realizan comprobaciones para corroborarlo. Si esas comprobaciones dan resultados positivos, se declara como primo ese número.

Con este software, y la ayuda de muchos internautas, GIMPS ha conseguido 15 nuevos números primos de Mersenne, con lo que la lista actual de estos números contiene 49 primos. Además, se encargan de comprobar que no nos hemos dejado ninguno por el camino (recordad que no necesitamos conocer los primos anteriores a nuestro número-objetivo, por lo que, por poner un ejemplo, podría salirnos antes el que ocuparía el número 60 que el ocuparía en número 59 en la lista ordenada).

El primero que encontraron, a finales de 1996, fue el que citábamos en el primer párrafo del artículo: M_1398269. A día de hoy, GIMPS ha comprobado que la lista es exhaustiva hasta el número 45, pero todavía no se sabe si desde ahí hasta el mayor conocido hoy nos hemos dejado alguno sin encontrar. Están en ello, y cuando todos los cálculos estén realizados lo anunciarán en su página web, donde también podéis ver, entre otras cosas, la lista completa de primos de Mersenne.

Volvamos ahora al título del artículo: El mayor número primo conocido. ¿Cuál es? Pues el número siguiente:

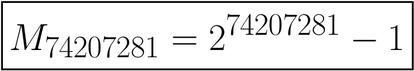
Sí, el exponente es 74207281. Es decir, que si quisiéramos calcularlo a mano tendríamos que multiplicar 2 por sí mismo esa cantidad de veces y después restar 1 al resultado. Casi nada.

Este número primo tiene la descomunal cifra de 22338618 dígitos. Sí, más de 22 millones de dígitos. Es un número enorme, enorme, enorme, mucho más grande de lo que una persona pueda imaginar. Para intentar hacernos una lejanísima idea sobre la magnitud de este número, pensad en lo siguiente:

Imaginad que tenéis un millón de euros (o pensad en ese millón si lo tenéis en realidad). Es mucho dinero, muchísimo, ¿verdad? Bien, pues un millón es un número que tiene solamente 7 cifras.

Y una última curiosidad sobre los primos de Mersenne. Está demostrado que cada número primo de Mersenne genera un número perfecto (que es un número que es igual a la suma de todos sus divisores excepto él mismo). Más concretamente, si M_p es primo, entonces el producto 2^{p – 1} · M_p es un número perfecto. Otro detalle que hace que estos números primos de Mersenne sean maravillosos.

Hablábamos unos párrafos más arriba sobre la búsqueda de una fórmula que genere siempre números primos. En la actualidad no se ha encontrado ninguna fórmula de ese tipo, y ni siquiera sabemos si existe tal fórmula. Lo que sí tenemos son expresiones particulares, como la de los números de Mersenne, que generan números primos para ciertos exponentes. Y no es la única, existen otras expresiones que también generan números primos de manera relativamente habitual y plataformas que ya las están estudiando utilizando su propio software. Os animo a que busquéis información sobre ellas y, si podéis, os unáis a las mismas. Quién sabe, quizás alguna de las personas que está leyendo este artículo sea el descubridor de, por ejemplo, el primer número primo de más de 100 millones de dígitos.