Lo más irracional de los racionales
Cuando el infinito hace acto de presencia, hasta las propiedades más básicas pueden dejar de cumplirse

A estas alturas ya estamos acostumbrados a escuchar frases tipo la siguiente:
Esto no es como en matemáticas, donde el orden de los factores no altera el producto
La cuestión es que esta afirmación no es del todo precisa, ya que eso de que el orden de los factores no altera el producto no pasa siempre en matemáticas. Cierto es que en la aritmética que utilizamos habitualmente, la de los números reales, sí es verdad que el producto de dos números no se altera si los cambio de orden (es decir, que la multiplicación de números reales de toda la vida cumple la propiedad conmutativa), pero eso no significa que siempre en matemáticas eso sea así. Los que hayan cursado matemáticas a nivel de bachillerato seguro que recuerdan un ejemplo muy claro de esto: el producto de matrices no es conmutativo. Esto es, si multiplico dos matrices en un cierto orden, digamos A · B, y luego las multiplico en el orden contrario, B · A, en general no obtendré el mismo resultado (de hecho, que una de las multiplicaciones se pueda hacer no nos garantiza que se pueda hacer la otra).
Ahora, si hablamos de sumas en vez de hablar de productos la cosa cambia en las matrices. Ahora sí que da igual en qué orden sumemos dos matrices (que se puedan sumar, se entiende), en ambos casos obtendremos el mismo resultado. De hecho sabemos más sobre ese resultado, en particular que será una matriz del mismo tipo que las dos que hemos sumado.
Lo mismo pasa con muchos de los conjuntos de números que conocemos. Por ejemplo, si sumamos dos números naturales siempre obtenemos como resultado un número natural, si sumamos dos números enteros conseguiremos un número entero y al sumar dos números racionales obtendremos, con total seguridad, un número racional como resultado de dicha operación. Esto no pasa con todas las operaciones, ya que, por ejemplo, al restar dos números naturales podríamos obtener un número que no es natural. Y tampoco ocurre con la suma en todos los conjuntos numéricos más o menos conocidos, ya que al sumar dos números irracionales no tenemos garantizado que vayamos a obtener un número que también sea irracional.
Cuando esto ocurre con un conjunto y una operación, en matemáticas decimos que el conjunto es cerrado para dicha operación (por lo de que si operamos no nos salimos del conjunto). En concreto, tenemos que los números racionales (el conjunto de todas las fracciones con numerador y denominador enteros) es un conjunto cerrado para la suma, como hemos comentado antes.
Con esto ya nos metemos más a fondo en la cuestión que vamos a tratar en este artículo: si sumo dos racionales obtengo siempre un racional. Pero esto no solamente ocurre si sumo dos, sino que también pasa si sumo más. Es decir: si sumo una cantidad cualquiera de números racionales, el resultado también es un número racional…
…siempre que la cantidad de números racionales que estemos sumando sea finita. Si sumamos 5 números racionales obtendremos un racional, y lo mismo ocurrirá si sumamos 20, si sumamos 100 o si sumamos 500000 millones de números racionales. Pero, ¿qué ocurre si sumamos infinitos números racionales? Pues…que hay que tener más cuidado a la hora de analizar cómo será el resultado.
Si os paráis a pensar cómo podría ser el resultado de sumar infinitos números racionales, es posible que la primera idea que os venga a la cabeza es que dicho resultado sería infinito. Pero hay que tener en cuenta que tenemos racionales positivos y negativos. ¿Seguís pensando lo mismo?
Bien, vamos a pasar de los negativos y a ceñirnos exclusivamente a los racionales positivos. Ahora sí, ¿verdad? Ahora sí que siempre obtendremos infinito como resultado…
…pues no, hay casos en los que al sumar infinitos números racionales nos queda de resultado un número (y no infinito). Por ejemplo, si sumamos 1/2, 1/4, 1/8, 1/16, (esto es, los inversos de las potencias de 2), el resultado es 1:
Esta suma infinita es un ejemplo de lo que en matemáticas se denomina serie numérica. En este caso se trata de una suma de infinitos números racionales cuyo resultado es también un número racional, algo que podría esperarse dado que, como comentamos antes, los números racionales son un conjunto cerrado para la suma (sí, es verdad, debería ser más preciso con las series y sus sumas, pero he preferido no meterme demasiado en los detalles técnicos).
Por supuesto que hay casos en los que el “resultado” es infinito, como éste:
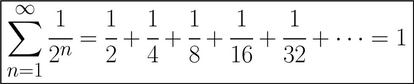
pero, como hemos visto, no siempre es así.
A la vista de lo comentado ya, y apoyados en el primero de los resultados que os he enseñado, no sería descabellado pensar que si sumo infinitos racionales obtendré siempre como resultado un número racional (excepto en los casos en los que nos queda infinito), ¿verdad?
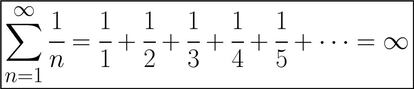
Pues lo “sorprendente” es que no siempre es así, y hay muchos ejemplos que lo corroboran. Uno de los más conocidos, sin duda, es el famosísimo problema de Basilea, que dice lo siguiente:
La suma de los inversos de los cuadrados de los números naturales es un número irracional. Concretamente, el cuadrado de Pi dividido entre 6.
Es decir, que si yo sumo los números racionales 1/1,1/4,1/9,1/16,1/25, etc, el resultado no es racional, sino irracional. Y, además, sabemos exactamente cuál es:
Y, como decía, no es el único ejemplo (por cierto, aquí tenéis una demostración de ese resultado). Con sólo números positivos tenemos más ejemplos del estilo al anterior, como éste:
Y también la suma que nos da como resultado el número e (que, como sabemos, es irracional):
Y si metemos también números negativos, tenemos otros ejemplos bastante interesantes, como la denominada serie de Leibniz:
Curioso, ¿verdad? Por todo ello he titulado así este artículo: lo más irracional de los racionales es que sumando racionales podemos obtener un resultado irracional.

Algo más complicado sería responder a la pregunta de por qué ocurre esta “rareza”. Bien, pues la cuestión es que “sumar” infinitos términos en el sentido de las series numéricas no es realmente “sumar”. No estamos realizando una suma habitual, sino que en realidad estamos calculando lo que en matemáticas se denomina límite de una sucesión (para los iniciados en el tema de las series, estamos calculando el límite de la sucesión de sumas parciales de la serie), y el límite de una sucesión no tiene por qué tener las mismas características que los números que forman dicha sucesión.
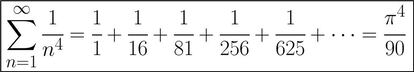
Pero todo esto es, posiblemente, demasiado avanzado para un artículo en el que os quería mostrar algo curioso que ocurre cuando introducimos el infinito en un lugar habitual para nosotros: las sumas de números racionales. Espero que os haya resultado interesante y que os sirva como ejemplo de que cuando aparece el infinito, en muchas ocasiones ocurren cosas “extrañas”…

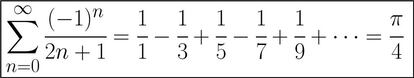
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































