Königsberg, Euler y dibujos en un solo trazo
Te mostramos cuándo y cómo puedes recorrer todas las líneas de un trabajo sin repetir ninguna
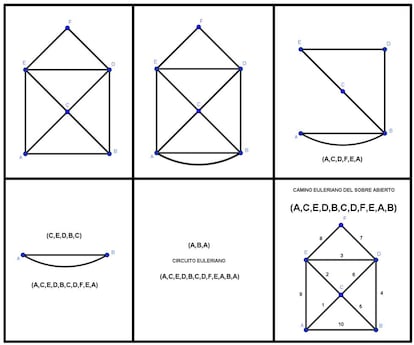
Con relativa frecuencia, podemos encontrar acertijos que nos proponen decidir si en cierta composición de líneas y puntos podemos recorrer, comenzando por uno de esos puntos, todas las líneas, pasando exactamente una vez por cada una de ellas. Vamos, que si podemos replicar el dibujo con un solo trazo sin repetir líneas. Dos ejemplos típicos son el sobre cerrado y el sobre abierto:
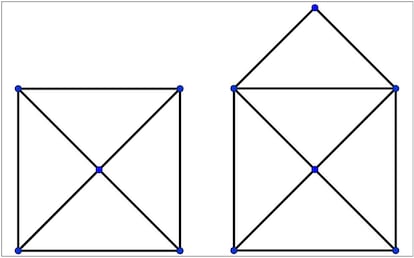
¿Se puede siempre? Y, en caso de que la respuesta sea negativa, ¿cuándo se puede? Hoy hablaremos sobre este tema, muy relacionado con los comienzos de una de las ramas de las matemáticas más importantes y con más aplicaciones de nuestro tiempo: la teoría de grafos.
La ciudad rusa de Königsberg (actual Kaliningrado) fue testigo de los primeros pasos importantes que se dieron en relación con los grafos. Y sus siete puentes fueron los culpables. La pregunta era si se podían recorrer todos estos siete puentes pasando por cada uno de ellos exactamente una vez, siendo la situación de los mismos como se muestra en la siguiente imagen. Tenéis los puentes rodeados con círculos azules y las cuatro regiones etiquetadas con las letras A, B, C y D:
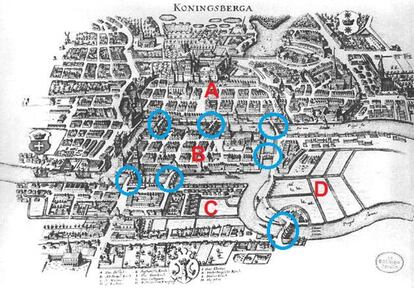
Fue Leonhard Euler quien dio respuesta a esta pregunta. Asignó a cada porción de tierra un punto, y a cada puente una línea, convirtiendo el problema de los puentes en un problema de teoría de grafos.
El grafo que obtuvo es el siguiente:
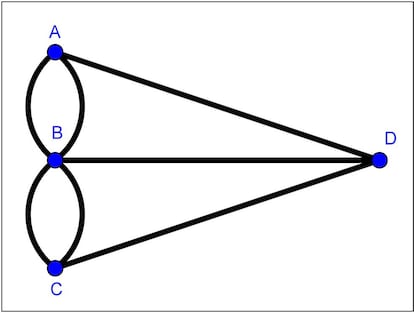
Como hay que comenzar en un vértice y terminar en otro (podría ser el mismo con el que se empieza), Euler observó que en los vértices intermedios deben concurrir un número par de aristas, para que por cada una con la que llegamos a dicho vértice haya otra por la que salgamos de él. Como en el grafo de los puentes de Königsberg tenemos en todos los vértices un número impar de aristas, la conclusión es que no se puede encontrar un camino que recorra todos los puentes pasando por cada uno de ellos exactamente una vez.
Teoría de Grafos
Un grafo es un conjunto de puntos, llamados vértices, y un conjunto de líneas, llamadas aristas, que conectan un par de puntos. Una construcción tan simple, en primera instancia, tiene multitud de aplicaciones, daba la potencia que tienen los grafos para modelizar situaciones reales.
Es interesante destacar que la teoría de grafos no se ocupa de las propiedades geométricas del grafo (como la forma o el tamaño), sino por sus propiedades topológicas (más generales), como la conexión.
La cuestión ahora es determinar qué condiciones tiene que cumplir un grafo para que sí se pueda encontrar un camino como el que estamos buscando. Aunque con lo dicho hasta ahora ya se puede intuir, vamos a explicarlo a continuación.
En todo lo que hemos comentado hasta ahora, estamos tratando con grafos no dirigidos, que son grafos en los que podemos recorrer cada arista en los dos sentidos (en los grafos dirigidos, las aristas se representan con flechas y solamente pueden recorrerse en el sentido que esté indicado por cada flecha), y con grafos conexos, que son grafos en los que cada vértice siempre puede conectarse con cualquier otro mediante un camino de aristas. En este tipo de grafos, el grado de un vértice es el número de aristas que concurren en él. Tras esta definición, vamos con el teorema que nos dice cuándo podemos hacer lo que buscamos:
Teorema:
En un grafo no dirigido y conexo, podemos encontrar un camino que recorra todas las aristas pasando por cada una de ellas exactamente una vez si se da alguna de las siguientes situaciones:
1.- Todos los vértices tienen grado par. En este caso, podemos empezar en cualquiera de ellos, y acabaremos en ese mismo vértice.
2.- Dos de sus vértices tienen grado impar y el resto tiene grado par. Entonces, el camino buscado comenzará en uno de los vértices de grado impar y terminará en el otro.
El primero de ellos se denomina circuito euleriano (porque comienza y termina en el mismo vértice), y el segundo camino euleriano.
Con este resultado ya podemos responder a lo que preguntábamos al principio del artículo: no podemos encontrar un camino de este tipo que recorra el sobre cerrado (tiene cuatro vértices con grado impar) y sí podemos encontrar dicho camino en el sobre abierto (tiene dos vértices con grado impar).
Ahora que tenemos el cuándo (sabemos cuándo podemos recorrer un grafo de la forma descrita), lo interesante sería saber el cómo. Cierto es que en un grafo con pocos vértices y pocas aristas no es difícil encontrar el camino (o el ciclo) a ojo, pero cuando el número de vértices y el número de aristas crece la cosa se complica. Por ello, vamos a ver un método, atribuido a Carl Hierholzer, para encontrar un circuito euleriano (en grafos cuyos vértices tienen todos grado par) que luego usaremos también para encontrar un camino euleriano en grafos con exactamente dos vértices de grado impar.
Veamos cómo encontrar un circuito euleriano. Como todos los vértices deben tener grado par, podemos comenzar por el que queramos (y terminaremos también en él). Tomamos un vértice cualquiera, digamos A, como comienzo, y seguimos estos pasos:
1.- Buscamos un camino de aristas (sin repetir ninguna) que comience en A y acabe también en A. Apuntamos entonces la secuencia de vértices que hemos recorrido (que, evidentemente, comenzará en A y acabará también en A).
2.- Quitamos las aristas que hemos recorrido y los vértices aislados (vértices a los que no llega ninguna arista), si es que nos quedó alguno.
3.- Si todavía queda algo del grafo, tomamos un vértice por el que ya hayamos pasado y hacemos lo mismo que en el paso 1: buscamos un camino de aristas que comience en él y acabe también en él, y apuntamos la secuencia de vértices recorridos.
4.- Insertamos esta secuencia en la anterior. Por ejemplo, si la primera era (A,B,C,D,A) y la segunda es (B,J,L,B), nos quedaría (A,B,J,L,B,C,D,A). Después, quitamos aristas recorridas y vértices aislados.
5.- Repetimos los pasos 3 y 4 las veces que sea necesario, y vamos insertando las secuencias de vértices obtenidas. El camino que nos queda al final es un camino que pasa por todas las aristas exactamente una vez.
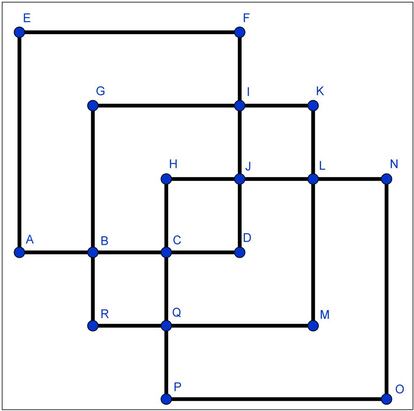
Veamos un ejemplo con un grafo concreto. Vamos a encontrar un circuito euleriano en el grafo que Lewis Carroll le envió por carta a una de sus amigas en 1869 y que Carlo Frabetti nos enseñaba en El sobre mágico de Lewis Carroll:
Podéis comprobar que todos sus vértices tienen grado par, por lo que podremos encontrar nuestro circuito euleriano. Elegimos un vértice para comenzar, por ejemplo el A y aplicamos el paso 1. Como da igual el camino cerrado que elijamos, tomamos el (A,E,F,I,G,B,A). Quitamos las aristas recorridas y los vértices aislados, como indica el paso 2. Nos queda el siguiente grafo:
Vamos con el paso 3: tomamos un vértice del grafo resultante por el que ya hayamos pasado y buscamos un camino cerrado como en el primer paso. Por ejemplo, elegimos el B y recorremos el camino (B,R,Q,M,L,J,H,C,B). Y ahora, como comenta el paso 4, insertamos esta secuencia de vértices en la primera. Nos queda la secuencia siguiente:
(A,E,F,I,G,B,R,Q,M,L,J,H,C,B,A)
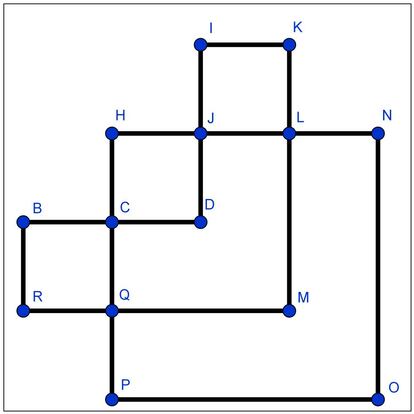
Quitamos aristas ya recorridas y los vértices que quedan aislados y nos queda el siguiente grafo:
Y, como puede verse, aplicando el procedimiento una vez más ya hemos terminado. Elegimos, por ejemplo, el vértice Q y tomamos el camino (Q,C,D,J,I,K,L,N,O,P,Q). Con ello, ya hemos recorrido todas las aristas del grafo exactamente una vez. Insertamos esta secuencia en la anterior y ya tenemos nuestro circuito euleriano:
(A,E,F,I,G,B,R,Q,C,D,J,I,K,L,N,O,P,Q,M,L,J,H,C,B,A)
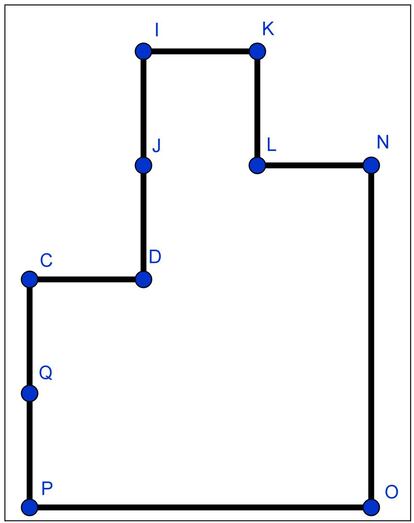
Posiblemente, sea interesante que os dibujéis el grafo en un papel y sigáis el camino obtenido tachando las aristas que vayáis recorriendo, para comprobar que en realidad se trata de un circuito euleriano. También podéis buscar otros posibles circuitos eulerianos, ya que, evidentemente, ésta no es la única opción posible.
Veamos ahora cómo encontrar un camino euleriano en un grafo que tenga exactamente dos vértices de grado impar. Si llamamos A y B a estos dos vértices, la clave es dibujar una nueva arista que una A con B (aunque ya hubiera una). Con ello conseguimos un grafo cuyos vértices tienen todos grado par, y podemos aplicar el proceso descrito anteriormente. Solamente hay que tener cuidado con un par de cosas. La primera es que el vértice elegido para comenzar sea uno de los dos que tienen grado impar al principio, el A o el B. Y la segunda es que, durante el proceso, vayamos eligiendo caminos que no contengan a la arista que hemos añadido. Lo más conveniente es que esa arista quede para el final, que sea la última arista recorrida. Así, cuando tengamos la secuencia de vértices del circuito euleriano, simplemente tenemos que eliminar el último vértice (que será el vértice con el que comenzamos) y ya tenemos nuestro camino euleriano.
Veamos el caso del sobre abierto como ejemplo. Partiendo del grafo inicial, añadimos la arista que hace que todos los vértices sean de grado par y aplicamos el proceso comenzando con el vértice A. Al final tenéis el camino euleriano resultante, con las aristas numeradas según el orden en el que las hemos recorrido:
Ya tenéis procedimiento para proponer acertijos (con solución o sin ella) a los amigos y para resolver (si es que se puede) los que os puedan proponer.
