¿Es muy difícil (estadísticamente) no dar ni una?

El conocido como amigo invisible es un “juego” muy popular en grupos de amigos, familiares o compañeros de trabajos, sobre todo en épocas como la recientemente terminada Navidad. Aunque imagino que no habrá nadie que no sepa en qué consiste, creo que conviene recordar su funcionamiento:

Se escriben en papelitos los nombres de todos los participantes y se mezclan dichos papelitos. Después, cada participante escoge al azar uno de ellos y debe hacer un regalo a la persona cuyo nombre aparece en él. Si alguien coge el papel que tiene su propio nombre, el sorteo se repite.

Hoy vamos a hablar precisamente sobre esto último, sobre cuál es la probabilidad de que el sorteo no se tenga que repetir. Es decir, vamos a hablar sobre la probabilidad de que en el primer sorteo no haya nadie que coja el papelito con su propio nombre, sobre la probabilidad de que nadie “acierte” con su nombre. Antes de seguir, quizás sea interesante que penséis sobre cuál podría ser dicha probabilidad. Intentadlo, haced un pequeño ejercicio mental y pensad sobre ello.

Lo primero que podría venirnos a la mente cuando pensamos sobre este tema es que la probabilidad de que no haya ningún acierto con el nombre dependerá del número de personas que participan. Eso es cierto, y más o menos evidente, pero lo interesante de verdad es analizar qué comportamiento podría tener dicha probabilidad conforme aumenta el número de personas: ¿sube o baja? ¿Es pequeña o grande? ¿Fluctúa sin control o se va acercando a un cierto número? En este último caso, ¿a qué número? Tranquilos, responderemos a todas estas preguntas.

Metámonos ya en faena. Tenemos un cierto número N de participantes, numerados desde 1 hasta N. Si numeramos también los papelitos de la misma forma, un sorteo será válido cuando al 1 no le toque el 1, al 2 no le toque el 2, y así con todos. Vamos, cuando ninguno coincida consigo mismo.

La situación se puede plantear como la búsqueda de las permutaciones de N elementos para los cuales no hay ninguna coincidencia de posición. Es decir, las permutaciones de los números desde 1 hasta N en las cuales ninguno cae en su propia posición. Vamos a escribir dichas permutaciones como listas de números entre paréntesis, y analizaremos las posiciones de la lista y el número que hay en cada posición. Por ejemplo, la permutación (1,4,5,2,3) indica que al primero le ha tocado el 1, al segundo le ha tocado el 4, al tercero el 5, al cuarto el 2 y al quinto el 3.

Analicemos todos los casos posibles para algunos valores pequeños de N. Si participan 2 personas (sí, es un poco ridículo, pero en realidad es el primer caso que tiene algo de sentido), pueden ocurrir dos cosas: que a los dos les toque su propio nombre o que a cada uno le toque el nombre del otro. Escrito como permutaciones, las únicas son (1,2) (al 1 le toca el 1 y al 2 le toca el 2) y (2,1) (al 1 le toca el 2 y al 2 le toca el 1). Como buscamos las permutaciones en las que no haya coincidencias, sólo nos valdría la segunda. Y como hay dos opciones posibles, la probabilidad de que el sorteo no se tuviera que repetir sería de 1/2=0’5.

Supongamos ahora que participan 3 personas. En este caso, tenemos 6 posibles sorteos:

Como podéis ver (recuadrados en rojo), hay dos sorteos válidos en este caso. Como hay 6 opciones posibles, la probabilidad de que no se tenga que repetir el sorteo es de 2/6=0’333...

Analicemos ahora el caso en el que hay 4 personas. Ahora tenemos 24 sorteos distintos, de los cuales hay 9 que dan una situación en la que no tendremos que repetir la asignación de papelitos. Aquí tenéis todas las posibilidades, con los sorteos válidos recuadrados en rojo:

Hay 24 sorteos posibles, de los cuales nos valen 9. Por tanto, la probabilidad en este caso será 9/24=0’375.

Si participan más personas, el número de opciones posibles crece bastante. Para 5 personas hay 120 sorteos posibles, para 6 personas hay 720, para 7 hay 5040, para 8 serían 40320… En general, para N personas hay N! (N factorial) sorteos. Por ello, no vamos a analizar uno a uno cada caso, pero sí os voy a dar los valores de las probabilidades (redondeadas a 20 decimales) para los primeros 25 valores de N:

¿Os parece alta o baja? ¿Cuadra con lo que pensasteis en un principio? A mí siempre me ha parecido bastante baja…¡¡¡en el 63% de los casos tendremos que repetir el sorteo!!! Por tanto, si a partir de ahora hacéis el amigo invisible con 5 o más personas y tenéis que repetir, tened en cuenta que no os ha ocurrido nada raro, ni mucho menos. De hecho, es bastante probable que así ocurra.

Volvamos al número anterior, 0’367879…, el valor límite de la probabilidad cuando N crece indefinidamente. Este número, aparte de ser más bajo de lo que uno podría pensar, es bastante “especial”. Pero antes de desvelar el porqué, vamos a hacer algún comentario sobre el problema que nos ocupa y sobre cómo calcular las probabilidades en cada caso.

El problema de calcular la probabilidad de que no haya ninguna coincidencia se denomina habitualmente The Matching Problem (también podéis encontrarlo como Montmort’s Matching Problem, en honor a Pierre-Remond Montmort, que parece que fue el primero que lo estudió). Si llamamos X_n a la variable aleatoria que nos da el número K de coincidencias (en nuestro caso, el número de participantes que sacan el papelito con su propio nombre) para n personas, se puede comprobar que su función de probabilidad es la siguiente (podéis ver los cálculos en esta web de la Universidad de Alabama):

Como nosotros queremos que no haya coincidencias, en nuestro caso se tiene que k=0. Haciendo tender n a infinito, tenemos que nuestra función de probabilidad tiende a:

Es decir, la probabilidad de que no haya que repetir el sorteo tiende, conforme aumenta el valor de n, a 1/e. No me digáis que no es precioso.

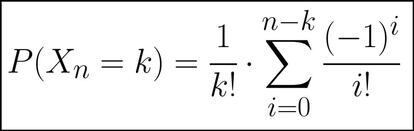
Y si en el caso del amigo invisible la probabilidad de que no haya que repetir el sorteo podría parecer baja, en otros ejemplos esta probabilidad de cero coincidencias puede parecer alta. Por ejemplo, imaginemos que en una fiesta se entrega a los asistentes sus abrigos de manera aleatoria. O que un profesor reparte unos exámenes de manera aleatoria entre sus alumnos. O que metemos tarjetas de regalo nominativas en sobres con nombre de forma también aleatoria. En todos estos casos, la probabilidad de que no haya ni una sola coincidencia es de 1/e. Esto es, en un 36’8% de los casos (aproximadamente) no daremos ni una. ¿No os parece muy alta?

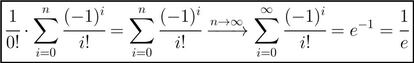
Y un último comentario respecto a este matching problem. En las situaciones que hemos descrito no hay reemplazamiento. Es decir, cada participante escoge un papelito y se lo queda (no lo devuelve), por lo que otro participante no puede coger el mismo papel, y lo mismo para el resto de ejemplos. Pero podríamos también estudiar estas situaciones con reemplazamiento. En el amigo invisible significaría que alguien toma un papelito, mira el nombre y lo devuelve al montón, por lo que otra persona podría coger el mismo más adelante.

¿Cómo quedaría el estudio de la probabilidad de cero coincidencias en este caso? Pues…exactamente igual: en el matching problem con reemplazamiento, la probabilidad de que no se tenga que repetir el sorteo es también 1/e. De nuevo, precioso.

La probabilidad, esa rama de las matemáticas a veces sencilla y en ocasiones muy complicada, y que en muchas circunstancias no sabemos interpretar correctamente. Por ello, podemos encontrar dentro de ella resultados curiosos y, por qué no, en cierto modo contrarios a nuestra intuición. Seguro que muchos de vosotros conocéis otros casos que sean dignos de mención en un comentario. Si es así habladnos de ellos, posiblemente salgan cosas interesantes para ser comentadas aquí en próximos artículos.