La paradoja de Bertrand: triángulos, circunferencias y probabilidad

Como ya sabéis los lectores de El Aleph, me encantan los triángulos, por lo que no me he podido resistir a hablaros de una curiosa paradoja relacionada con ellos de la cual tuve conocimiento hace ya unos años.

El tema que nos ocupa trata sobre circunferencias, triángulos y probabilidad. Y, por lo que parece, estos tres ingredientes forman una mezcla explosiva, matemáticamente hablando. Vamos a plantear la cuestión y después indagaremos en las posibles soluciones.

El enunciado de nuestro problema es el siguiente:

“Tomamos una circunferencia e inscribimos en ella un triángulo equilátero (triángulo con los tres lados y los tres ángulos iguales). Escogemos ahora una cuerda al azar (una cuerda es cualquier segmento que une dos puntos de la circunferencia). ¿Cuál es la probabilidad de que la longitud de dicha cuerda sea mayor que la longitud del lado del triángulo?”

En la imagen siguiente podéis ver un triángulo equilátero inscrito en una circunferencia y cuerdas de distintas longitudes:

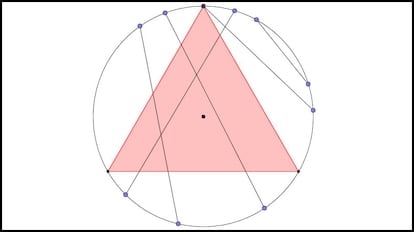
Este problema se conoce con el sugerente nombre de la paradoja de Bertrand, debido a que fue el matemático francés Joseph Bertrand quien la introdujo en su libro Calcul des probabilités en 1889. Que se le califique como una paradoja se va a entender enseguida.

Adentrémonos en la solución. Tomamos un punto cualquiera de la circunferencia, el que queramos. Como la posición en la que dibujemos el triángulo es indiferente, podemos hacer coincidir dicho punto con uno de sus vértices, digamos que el superior en la imagen anterior. Si ahora trazamos una cuerda, elegida al azar, desde ese vértice, puede ser que la cuerda llegue al arco de circunferencia inferior, con lo que la cuerda sería mayor que el lado del triángulo. Pero también puede ser que llegue a alguno de los dos arcos laterales, y entonces la cuerda sería menor que el lado. Ambas opciones están representadas en la imagen:

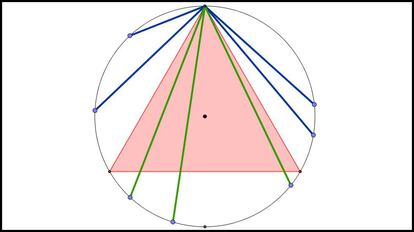
Como nuestro triángulo es equilátero, los tres arcos son iguales. Y como dos de los arcos dan cuerdas menores y uno da cuerdas mayores, la probabilidad de que la cuerda sea mayor que el lado del triángulo es 1/3.

Cuestión solucionada, ¿verdad? Pues la cosa es que no. Veamos el problema de la siguiente forma: tomemos un radio cualquiera del círculo y giremos el triángulo hasta que uno de los lados sea perpendicular a dicho radio. La cuerda la trazamos escogiendo al azar un punto de dicho radio y trazando la cuerda que pasa por dicho punto y es perpendicular al radio, como aparece en la imagen:

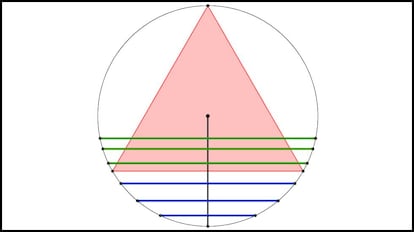
Como se puede ver, la cuerda es mayor que el lado del triángulo si pasa por un punto de la parte interior del radio, y menor que el lado si pasa por un punto de la otra parte del mismo. Como el lado del triángulo divide al radio en dos partes iguales, se tiene que la probabilidad de que la cuerda sea mayor que el lado del triángulo es 1/2.

Vaya, pues parece que la cosa no es tan sencilla como podía parecer. Y lo peor (o lo mejor) es que aún hay más.

Tomemos ahora un punto al azar dentro del círculo, y tracemos la cuerda que tiene a ese punto como punto medio. Si dibujamos ahora el círculo inscrito en el triángulo (que tiene de radio la mitad que el radio del círculo inicial), se tiene que si el punto escogido cae dentro de este círculo inscrito, entonces la cuerda es mayor que el lado de nuestro triángulo; y que si el punto está fuera de dicho círculo inscrito, entonces la cuerda es menor que el lado. Podéis verlo en la siguiente imagen:

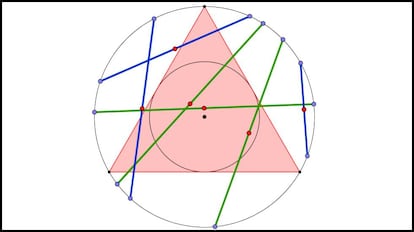
Calculamos entonces la probabilidad dividiendo el área favorable, la del círculo inscrito, entre el área total, la del círculo inicial. Si R es el radio del círculo inicial, tenemos que el área total es πR² y que el área del círculo inscrito es π(R/2)². Realizando la división correspondiente tenemos que la probabilidad de que la cuerda sea mayor que el lado del triángulo es 1/4.

Recapitulando, tenemos un problema de probabilidad con tres soluciones distintas, hecho que choca frontalmente con la propia concepción de probabilidad. ¿Qué ocurre? La solución clásica es que necesitamos definir claramente qué entendemos por elegir una cuerda al azar. En el momento en que la elección al azar esté bien definida, podremos responder a la pregunta que nos plantean.

Pero claro, esta solución se queda algo corta. Y no soy el único que lo piensa, ya que, a pesar de que el problema se planteó y se trató hace más de 100 años, han sido varios los matemáticos que se han interesado por él y que han publicado trabajos al respecto.

Uno de los que me parecen más interesantes es el de Edwin Jaynes, que en 1973 publicó The Well-Posed Problem. En dicho trabajo comenta que en este problema debería aplicarse el llamado principio de máxima ignorancia, que en nuestro caso implica que el problema debería ser invariante frente a cambios de escala y traslaciones de la circunferencia inicial. Esto es, si tomamos circunferencias menores o trasladadas, la distribución de las cuerdas debería ser igual a la que hay en la circunferencia inicial. Analizando las distribuciones de las cuerdas de los tres métodos (imágenes tomadas de aquí):

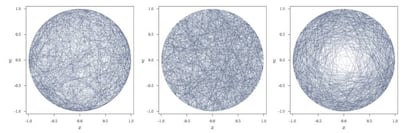
se llega a la conclusión de que el único método que mantiene invariantes la escala y la traslación es el método 2.

Pero Jaynes no ha sido el único que se ha interesado por la paradoja de Bertrand en los últimos años. En 2014, Diederik Aerts y Massimiliano Sassoli de Bianchi publicaron Solving the Hard Problem of Bertrand’s Paradox, en el que, mediante un nuevo enfoque, acaban llegando a unos resultados numéricos que están de acuerdo con los resultado de Jaynes.

¿Resuelve esto nuestra paradoja? Pues la verdad es que no está demasiado claro. Parece que en los últimos tiempos muchos coinciden en que el método 2 sería el más aconsejable, pero, al menos yo, no encuentro razones suficientes para desechar los otros dos métodos. Y tampoco para que, visto lo visto, pudiera existir algún otro método que arrojara un resultado distinto. ¿Qué os parece a vosotros?