Y el premio al camino más corto es para...

…pues depende.

¿Cómo que “depende”? El camino más corto ha sido la línea recta de toda la vida, ¿no? ¿Entonces?

Pues eso…que depende. Más concretamente, depende de qué entendamos por “más corto”, que no tiene por qué significar siempre lo mismo.

Vamos a poner un ejemplo. Imaginemos que queremos ir desde el trabajo a nuestra casa en bici (nos preocupamos por el medio ambiente) y queremos llegar lo antes posible (estamos deseando llegar a nuestro amado sofá después de una larga jornada laboral). Analizando los posibles caminos que podemos seguir, nos quedamos con estas dos opciones.

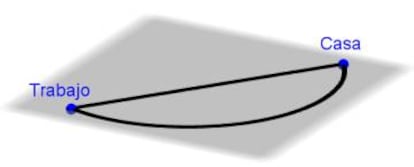
Suponiendo que no hay desnivel en ninguno de ellos y que ambos están perfectamente asfaltados, lo más probable es que eligiéramos el camino recto.

Ahora imaginad que ese camino recto es de verdad un “camino”: es de tierra, tiene piedras y baches a montones…Vamos, que es complicadísimo manejarse con la bicicleta a través de él. Sin embargo, el otro continúa estando perfectamente asfaltado, comodísimo para nuestro viaje en dos ruedas. ¿Seguiríamos eligiendo el recto? Posiblemente no, ya que, como hemos dicho ya, queremos llegar cuando antes a casa.

Con esto quiero dejar constancia de que no siempre no interesará el camino de menos longitud, porque igual no siempre ese camino es el más rápido. Y aquí está la clave de la interpretación de “más corto” de la que hablábamos al principio: “más corto” puede significar “menor longitud” o “menor tiempo”, según el caso.

Seguro que más de un lector está pensando que hemos hecho algo de trampa, en el sentido de que hemos cambiado las condiciones de uno de los caminos. Sí, eso de dar como opción un camino prácticamente intransitable podría considerarse, en parte, como una trampa. Por eso, vamos a intentar igualar las condiciones con el siguiente problema:

Imaginemos que queremos mover un objeto desde el punto A al punto B, colocados según esta imagen.

Queremos que el objeto recorra una cierta curva que una A con B. Suponemos que soltamos dicho objeto desde A para que se desplace por la curva (es decir, no lo empujamos ni nada parecido) impulsado solamente por la acción de la gravedad. La pregunta es la siguiente: ¿cuál sería la curva con la que el objeto tardaría menos en llegar? Esto es, ¿cuál es la curva más rápida?

Seguro que más de uno se ha dicho algo como esto: “¿Cuál va a ser? La línea recta” (sí, una recta es una curva; en concreto, es una curva con curvatura cero, una curva que no se curva). Y es normal, yo también creo que ésa sería la respuesta más habitual si planteamos esta situación a alguien. Pero no, lo curioso del asunto es que la línea recta no es la curva más rápida en este caso.

Este problema de encontrar la curva que desciende más rápido de un punto a otro en un plano vertical, característica conocida como “braquistocronía”, fue planteado por Johann Bernoulli en 1696. Y la solución al mismo resultó ser una curva denominada cicloide.

La cicloide es la curva que describe un punto de una circunferencia al girar por una recta (sin deslizarse). Por si no os quedado totalmente clara la definición, os dejo este gif bastante esclarecedor.

Esta curva había sido estudiada anteriormente por muchos matemáticos, como Galileo, Mersenne o Roberval. Gracias a estos estudios se descubrieron algunas características interesantes de la misma, como la longitud de un arco de cicloide (que es cuatro veces el diámetro de la circunferencia que la genera) o el área encerrada también por un arco de cicloide (que resulta ser tres veces el área de dicha circunferencia), pero fue a partir del planteamiento del problema por parte de Johann Bernoulli cuando se encontró esta interesante propiedad de la braquistocronía de la cicloide.

Por cierto, la historia de la resolución del problema en sí también tiene su interés. Además del mismo Johann, fueron cinco los matemáticos que enviaron sus soluciones al problema: Jakob Bernoulli (hermano de Johann), Tschirnhaus, Leibniz, L’Hopital y Newton. El día que éste último tuvo conocimiento del problema, se quedó despierto toda la noche para resolverlo y poder enviar la solución al día siguiente. Vamos, que tardó menos de un día en encontrar la respuesta; Johann Bernoulli tardó dos semanas…

Por tanto, está demostrado matemáticamente que la cicloide gana a cualquier otra curva (recta, parábola o cualquier otra) en rapidez de descenso, pero seguro que mucha gente todavía puede mostrarse recelosa. Para hacer desaparecer ese recelo, qué mejor que un vídeo mostrando su mayor rapidez frente a un segmento de recta. En él podemos ver cómo se sueltan a la vez dos bolitas para que rueden por un segmento de recta y por un arco de cicloide, y después se hace lo mismo con dos cochecitos de juguete (los lanzamientos comienzan sobre el segundo 48):

Pero la cosa no queda ahí. La cicloide tiene otra curiosísima propiedad, conocida desde 1659 gracias a Christiaan Huygens. La cuestión es la siguiente:

Supongamos que tenemos dos puntos A y B, situados en la horizontal, y representamos un arco de cicloide de A a B por debajo de dicha horizontal (es decir, el que podríamos llamar vértice de la cicloide es el punto más bajo de la misma). En esta situación, si soltamos un objeto para que se desplace por dicho arco de cicloide únicamente bajo el efecto de la gravedad, se tiene que dicho objeto llegará el punto más bajo siempre en el mismo tiempo, independientemente del punto inicial en el que lo coloquemos.

Es decir, da igual el punto desde el que soltemos el objeto, siempre tardará lo mismo en llegar al punto más bajo. Esta propiedad se conoce con el nombre de tautocronía.

Seguro que ahora también hay personas que no lo ven muy claro, que no llegan a creerse que esta propiedad pueda ser cierta. Pues sí amigos, para la tautocronía también tenemos vídeo (la primera bola sitúa el punto más bajo; el lanzamiento podéis verlo a partir del segundo 40):

La cicloide tiene más propiedades y características interesantes, pero nosotros nos vamos a quedar aquí. La idea en este caso era encender la mecha de la curiosidad. Espero haberlo conseguido.