15 il·lusions òptiques que faran que no tornis a confiar en els teus ulls

Les il·lusions òptiques són percepcions visuals que no s'ajusten a la realitat del món que ens envolta. No només són jocs, sinó que ens ajuden a entendre com veiem i com reconstruïm el món.

I és que les il·lusions òptiques posen de manifest que els ulls no són càmeres de vídeo que enregistren tot el que passa, sinó que el cervell interpreta i reelabora la informació que ens proporcionen els sentits. La majoria de vegades això no ens causa problemes. Al contrari, ens ajuda. Però en determinades circumstàncies, no tenim prou informació o ens influeix el context i aquesta reconstrucció és ambigua o defectuosa. Aquí en tenim 15 exemples, molts de clàssics.

1. Organització, organització!

Algunes de les il·lusions òptiques juguen amb com organitzem la nostra percepció. Quan la informació és ambigua, no sabem si estem veient un ànec o un conill, o una calavera o una senyora, com en aquesta il·lusió creada el 1892 per l'artista Charles Allan Gilbert i amb moltes versions posteriors.

2. La il·lusió de Zöllner

Amb poques línies n'hi ha prou per confondre'ns. Com en aquesta il·lusió descoberta per l'astrofísic alemany Johann Karl Friedrich Zöllner el 1860. Tot i que aquestes rectes són paral·leles, sembla que s'inclinen per influència de les línies diagonals.

3. La paret de la cafeteria

Aquest efecte és semblant. Les línies són paral·leles, tot i que no ho sembla per la disposició dels quadres i el contrast entre el blanc i el negre, que dificulten que es vegi bé la línia que separa les files i que fan que cada quadre sembli més ample en un dels extrems. Es coneix des del 1898, però la va popularitzar als anys setanta Richard Gregory, que li va posar aquest nom perquè la va veure a la paret d'una cafeteria de Bristol. Hi ha un edifici de Melbourne que juga amb aquest efecte.

4. El fals entrellaçat

Si anem cap a les línies corbes, ens topem amb aquesta il·lusió creada pel psicòleg italià Baingio Pinna el 2002. Aquestes línies sembla que es creuïn, però es tracta de cercles concèntrics.

Els cercles estan creats amb quadrats blancs i negres que s'alternen en color i en inclinació. És a dir, el cervell rep pistes que porten a inferir que es tracta d'una espiral, tot i que en realitat són cercles.

5. Quin és més gran?

No som gaire bons fent una estimació a ull nu de les longituds i grandàries. Un exemple és la il·lusió de Jastrow, descoberta pel psicòleg nord-americà Joseph Jastrow el 1889. Les dues barres tenen la mateixa grandària, encara que no ho sembli.

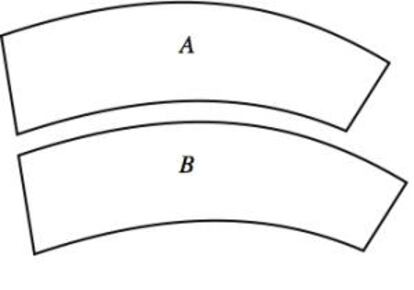
D'acord, no t'ho creus. Aquest vídeo potser t'ajuda a veure-ho més clar.

6. Les taules de Shepard

Un exemple semblant és el de les taules de Shepard. Quina d'aquestes dues taules és més ampla? I quina és més llarga?

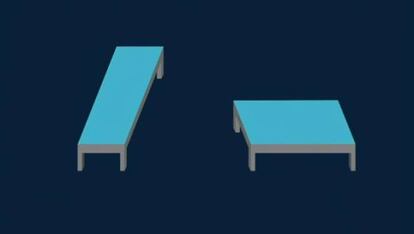
Les dues són iguals.

Com expliquen a Mental Floss, percebem les línies verticals més llargues que les horitzontals, tot i que tinguin la mateixa mida, per un efecte descrit pel fisiòleg alemany Adolf Fick el 1851. En aquesta il·lusió influeix també la sensació de perspectiva. Interpretem els dibuixos com dues taules en un espai en tres dimensions, oblidant que són superfícies planes, i la primera ens sembla així més llarga que la segona.

(Les imatges són d'una conferència de Michael Abrash, responsable d'investigació i desenvolupament de la plataforma de realitat virtual Oculus).

7. L’habitació d’Ames (i d’El senyor dels anells)

Però pel que fa a la perspectiva, no hi ha res millor que l'habitació d'Ames, anomenada així pel psicòleg nord-americà Adelbert Ames, que va crear una habitació que sembla normal si es veu des del davant i al centre, però que en realitat és trapezoïdal: les parets, el terra i el sostre estan inclinats. El disseny del terra també sol ajudar a crear aquesta il·lusió. Aquest seria el pla:

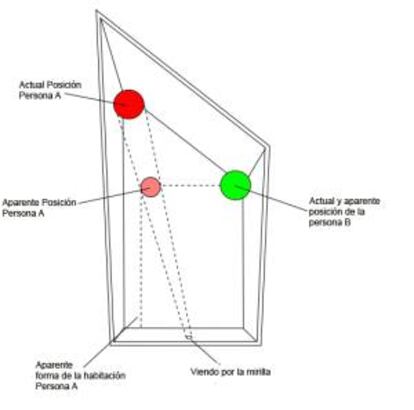
I així és com es veu.

Normal que s'hagin fet servir "perspectives forçades" similars a la d'aquesta habitació a El senyor dels anells per jugar amb la grandària de hobbits, nans i altres personatges. Aquí hi ha el vídeo.

8. Aquests quadres no poden ser del mateix color!

Els quadrats A i B són del mateix to de gris. Es tracta de la famosa il·lusió d'Adelson.

Aquest gif ajuda a veure-ho millor.

El cervell compensa el color dels quadres aplicant la constància parcial del color. Si són del mateix color, tot i que B és a l'ombra d'un cilindre, això vol dir (per al cervell), que aquest quadre ha de ser més clar. També influeixen els quadres que hi ha al voltant de cadascun. I és igual que sapiguem que són del mateix to: no hi ha manera de veure'ls així.

9. I aquests cubs tampoc!

Un altre exemple semblant és el d'aquests cubs. El de dalt sembla gris fosc i el de baix, blanc. Ara tapa amb un dit la separació. Efectivament, els dos són del mateix color. I una vegada traiem el dit, tornem a veure dos tons de gris diferents.

Es tracta de l'efecte Cornsweet: "El sistema visual pren el gris fosc i el blanc de les vores i l'estén a través dels quadrats", expliquen a Science Blogs, on s'esplaien més en les causes i en posen més exemples.

10. Una espiral és verda i l’altra és... blava?

El context també influeix en quins colors veiem. Ho vèiem fa poc en l'exemple de les píndoles blava i vermella (i sobretot en el cub de Rubik que apareix a la mateixa peça). El que passa amb aquesta imatge és semblant. Fixem-nos en les espirals verda i blava.

Resulta que les dues són del mateix color, però pensem que són diferents pel context on apareixen: les verdes, creuades per franges taronges i les “blaves”, per franges magenta, com expliquen a Discover Magazine, on assenyalen que la il·lusió està extreta del web del psicòleg Akiyoshi Kitaoka.

Si passem la imatge per Photoshop o per qualsevol programa que reconegui el color, podem comprovar que el codi RGB de les dues espirals és 0, 255, 150 (un to de verd). Però, com en la il·lusió d'Adelson, resulta impossible veure les dues espirals del mateix color.

11. Com veure en color una imatge en blanc i negre

Un altre efecte de colors interessant és el provocat per la fatiga de retina. Quan ens exposem a una gran quantitat de llum d'un determinat color, els cons que perceben aquesta llum es cansen i deixen de respondre per uns segons. Això provoca, per exemple, que puguem veure en color la imatge d'aquest gif. Només cal mirar el punt negre. I esperar.

12. Segueix el punt 

Una il·lusió que combina color i moviment és aquesta creada el 2005 per l'expert en visió Jeremy Hinton. Centrant la visió en la creu del centre, es pot veure un cercle verd a l'espai que van deixant en blanc els punts magenta. Amb la suficient concentració fins i tot poden desaparèixer aquests altres cercles. No només es tracta de la fatiga de retina, que segons explica el fisiòleg Michael Bach ens porta a veure el color complementari, sinó que també s'hi afegeixen la il·lusió de moviment i l'efecte Troxler, que fa que s'esvaeixin les imatges borroses si apareixen en el camp de la nostra visió perifèrica.

13. La quadrícula que fa pampallugues

Tot i que si el que t'agrada és veure coses que no són aquí, el millor és la il·lusió de la quadrícula que fa pampallugues (semblant a la de Hermann i descoberta per E. Lingelbach el 1994). N'hi ha prou amb fixar-se en una de les interseccions (qualsevol), per comprovar que no hi ha cap punt negre. Encara que allà n'hi ha un altre. I allà. I allà.

14. Els cercles que es mouen, però no es mouen (però es mouen)

Els colors i les ombres poden fer l'efecte que aquests cercles es mouen, ja que els patrons de colors imiten el tipus d'informació que rebem quan veiem un objecte en moviment. Aquesta il·lusió afecta la visió perifèrica: si ens fixem només en un dels cercles, veurem que no està quiet. En tot cas, aquesta imatge, basada en el treball del psicòleg Akiyoshi Kitaoka, no és un gif. 

15. El tren que ve (o se’n va)

Pero ja n'hi ha prou d'il·lusions òptiques. Serà millor que torni a casa amb metro. El problema és que no sé si el tren ve o se'n va. Com que la imatge és en dues dimensions, al cervell li costa saber si el tren entra o surt del túnel. És fàcil veure la imatge amb els dos sentits de la marxa de forma molt seguida.