¿Quién va a ganar la Eurocopa? Así están las predicciones de nuestro modelo estadístico
Consulte las probabilidades de cada selección para ganar el torneo
¿Qué opciones tiene cada selección de ganar la Eurocopa? Estamos enfrentando esa pregunta simulando el torneo miles de veces cada día, conforme avanza. Así podemos calcular qué probabilidad tiene (y tenía) cada equipo de alcanzar cada fase o llevarse el torneo.
| SELECCIÓN |
|---|
| ÍNDICE EP | OCTAVOS | CUARTOS | SEMIFINALES | FINAL | GANA |
|---|
La tabla anterior dice qué equipos son favoritos y en qué medida. Los datos también demuestran la enorme incertidumbre del terreno de juego. El fútbol es un deporte imprevisible, pero nuestro modelo lo sabe: por eso, aunque Francia era la favorita al empezar la Eurocopa, el 80% de las veces acababa eliminada en las simulaciones del modelo (como efectivamente ocurrió).
Esta es la tercera vez que publicamos predicciones de un torneo, después de los mundiales de 2018 y 2022. La metodología completa se puede leer al final, aunque la esencia del modelo es sencilla. Lo alimentamos con datos de resultados de cada selección y de la calidad de sus jugadores, para luego simular el campeonato miles de veces.
Cómo han cambiado los favoritos
Cada día actualizamos las predicciones y guardamos las anteriores. En el selector de la primera tabla se puede ver qué decía nuestro modelo en cada momento. Además, en este otro gráfico mostramos la evolución de nuestros pronósticos a lo largo del torneo:
Las predicciones durante la fase final
La tabla muestra los cruces jugados, y los más probables, con las opciones de cada equipo de vencer en esos duelos si están todavía por jugar.
Qué dicen otras predicciones
¡No somos los únicos haciendo pronósticos! Cada año hay más compañías, comunidades y aficionados que se animan a hacer sus números. En la tabla mostramos tres fuentes interesantes: el modelo estadístico de Opta, la empresa especializada en estadística deportiva, la predicción de un promedio de casas de apuestas, que suelen ser lo más preciso, y por último, la predicción de Metaculus, una comunidad de pronosticadores.
| SELECCIÓN |
|---|
| EL PAÍS | APUESTAS | METACULUS | OPTA |
|---|
¿Cómo funciona nuestro modelo?
Nuestras predicciones son el resultado de hacer miles de simulaciones. En cada partido, la probabilidad de que gane uno u otro equipo depende de sus estadísticas. Por ejemplo, si Francia juega contra Albania, la probabilidad de que gane el primero ronda el 83%.
El modelo tiene tres partes:
1. Métrica de fortaleza del equipo. Para medir esto usamos dos métricas: sus resultados recientes (medidos con un ránking Elo) y la calidad de sus jugadores (medida con su valor en euros, con datos de la web Transfermarkt).
2. Simulador de partidos. Hemos entrenado un modelo con miles de encuentros para, dados dos equipos y sus métricas de fortaleza, estimar cómo de probable es cada resultado. El modelo dice la probabilidad de victoria, empate y derrota; incluso la de cada marcador. Por ejemplo, en un duelo hipotético entre Francia y Albania, los resultados más probables son 2-0 y 3-0 con un 14% cada uno.
3. Simulador de la Eurocopa completa. Por último, lo que hacemos es simular el torneo partido a partido. Esto lo repetimos miles de veces, para tener 200.000 eurocopas posibles, y así poder estimar la probabilidad de cada evento.
A continuación respondemos algunas preguntas habituales con el modelo. Luego, damos más detalles de su funcionamiento.
Las preguntas frecuentes
Entonces, ¿decís que va a ganar Francia? No, no. Nuestro modelo dice que Francia es la selección con más probabilidades, pero también que tiene solo una opción entre cinco de ganar. Es importante interpretar bien esto: en realidad, su victoria es tan poco probable como ver fallar un tiro libre.
Estos datos vienen a demostrar que una Eurocopa es difícil de predecir. Y no es una sorpresa. Primero, es un torneo diseñado para que la suerte influya: no es una liga regular, no tiene playoffs, ni partidos de ida y vuelta. Segundo, las selecciones juegan pocos partidos importantes y su rendimiento es más incierto que el de un club. Y tercero, hablamos de fútbol, un deporte apasionante porque está lleno de sorpresas. Casi nadie se sentaría a ver un partido si el resultado estuviese decidido.
¿Habéis hecho esto antes? Sí. Usamos un modelo parecido en los mundiales de 2018 y 2022. Aquí podéis leer qué tal funcionó uno y otro. El modelo se ha demostrado bien calibrado: los resultados a los que dábamos una probabilidad entre 0% y 15% ocurrieron el 4% de las veces, por ejemplo, y aquellos con probabilidad 85% o 100% ocurrieron el 94% de las veces. En 2018, lo hicimos mucho mejor que el azar, mejor que el ranking FIFA y que dos grandes bancos (UBS y Goldman Sachs), aunque ganó Francia, que solo era nuestra sexta favorita al empezar. En 2022, la final la jugaron dos de los tres equipos que veíamos mejores, y batimos incluso a las apuestas.
¿Debería apostar usando vuestros pronósticos? No. Nuestro modelo es relativamente sofisticado y puede funcionar bien. Pero las apuestas han demostrado en el pasado que son muy difíciles de mejorar. Además, para no perder dinero no basta con batirlas, también hay que compensar el margen que se reservan las casas de apuestas al fijar los precios.
Los modelos estadísticos son útiles como referencia, por transparencia y porque nos permiten calcular detalles que las apuestas no responden. Pero, a la hora de acertar, las apuestas usan una aproximación híbrida: combinan modelos propios con el ajuste fino que hacen sus expertos, para considerar la información extra que poseen (como detalles de estilos de juego, estados de forma o lesiones).
Más detalles técnicos
Qué es un ranking Elo. Es una métrica que captura la fuerza de cada equipo según sus resultados. Cada equipo tiene cierta cantidad de puntos —sus puntos Elo—, y con cada partido se produce un intercambio. El ganador se lleva puntos del perdedor. Si la victoria es por sorpresa (porque se impone el equipo débil) los equipos se intercambian más puntos. Los rankings Elo funcionan bien y se usan cada vez más, en deportes y en videojuegos, por ejemplo, para organizar partidas entre jugadores de nivel parecido. Nuestro modelo usa el ranking Elo de la web Eloratings.
Por qué usamos el valor de las plantillas. Porque las selecciones juegan pocos partidos competitivos y eso dificulta medir su rendimiento antes de una gran cita. Una forma de añadir información al modelo es usar el valor en el mercado de fichajes de los jugadores que las componen. Tomamos los datos de la popular web Transfermarkt, ajustados por la edad de los jugadores (los mayores de treinta se abaratan por tener menos años de carrera por delante).
Cómo funciona el simulador de partidos. Hemos ajustado un modelo sencillo que estima los goles que marcará cada equipo en función de: 1) si es mejor o peor que su rival por puntos Elo, 2) si es mejor por valor de plantillas, y 3) si juega como anfitrión, fuera o en campo neutral. El modelo usa una distribución de tipo Poisson, que aproxima razonablemente los goles, y que se ha usado en modelos estadísticos y estudios académicos.
Al final, para nuestro modelo, para un partido en campo neutral, la probabilidad de que un equipo gane un partido depende de dos números: las diferencias con el rival en puntos Elo y valor de plantillas. El gráfico lo resume:
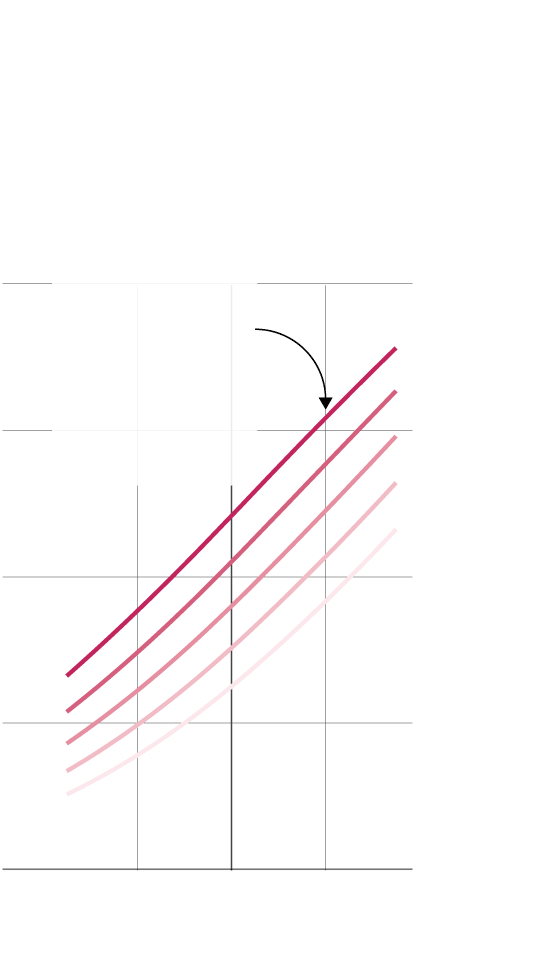
Un resumen del modelo. El gráfico muestra la probabilidad que tiene un equipo de ganar un partido en función de dos parámetros: las diferencia sobre su rival en puntos Elo y en valor económico de sus plantillas.
Un equipo con una plantilla 160 millones más cara que su rival y con 200 puntos más de Elo gana el 62% de sus duelos
80%
Diferencia de
valor de
160 millones
80 millones
60
0
-80 millones
-160 millones
40
20
0
−200
0
200
Diferencia de ELO
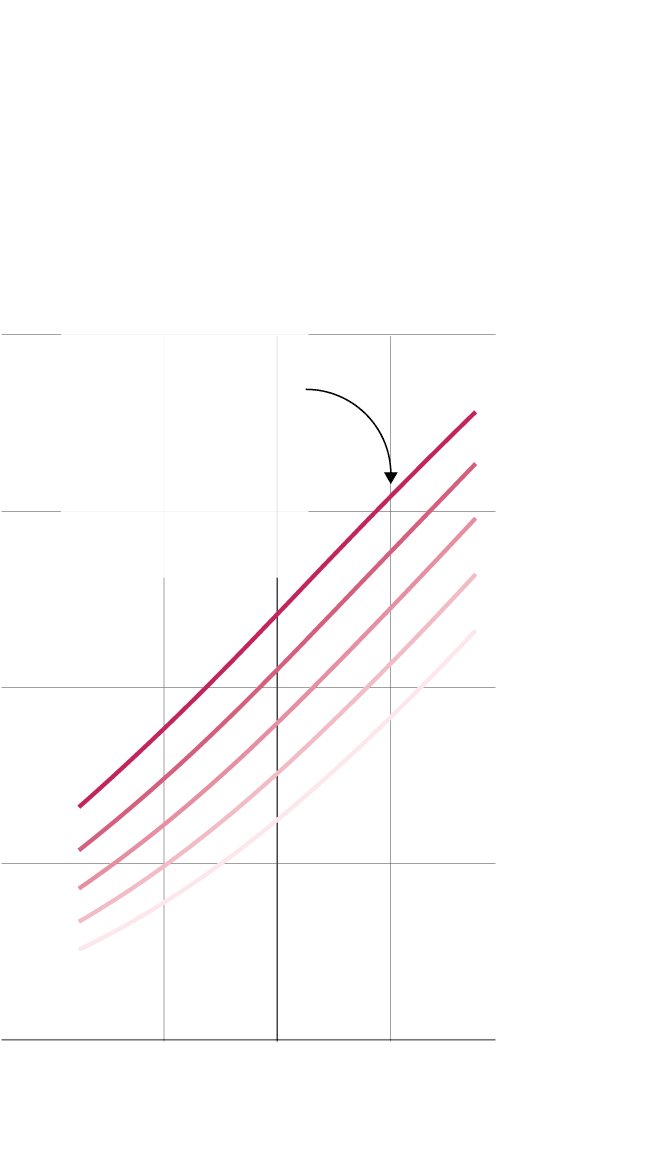
Un resumen del modelo. El gráfico muestra la probabilidad que tiene un equipo de ganar un partido en función de dos parámetros: las diferencia sobre su rival en puntos Elo y en valor económico de sus plantillas.
Un equipo con una plantilla 160 millones más cara que su rival y con 200 puntos más de Elo gana el 62% de sus duelos
80%
Diferencia de
valor de
160 millones
80 millones
60
0
-80 millones
-160 millones
40
20
0
−200
0
200
Diferencia de ELO
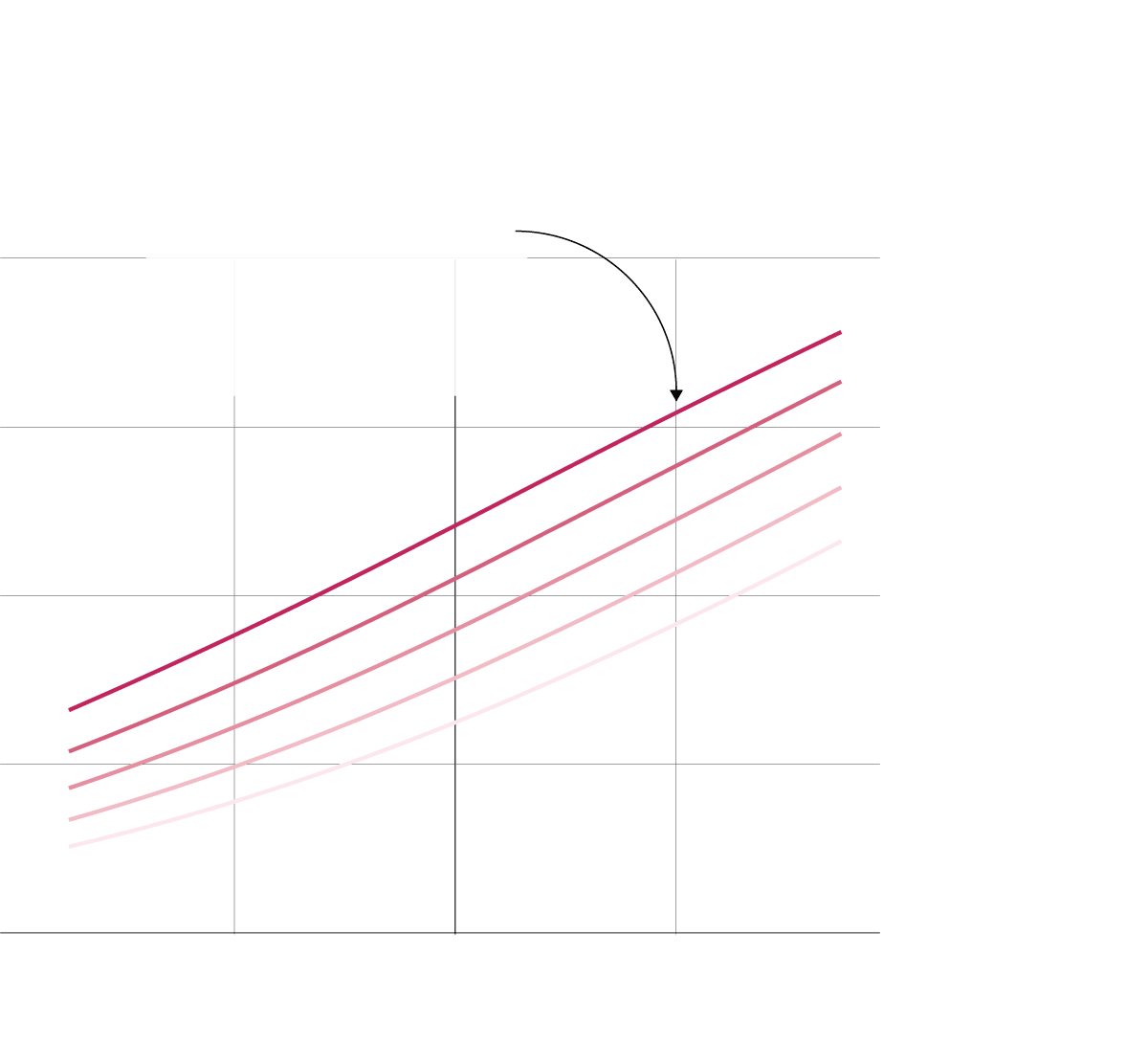
Un resumen del modelo. El gráfico muestra la probabilidad que tiene un equipo de ganar un partido en función de dos parámetros: las diferencia sobre su rival en puntos Elo y en valor económico de sus plantillas.
Un equipo con una plantilla 160 millones más cara que su rival y con 200 puntos más de Elo gana el 62% de sus duelos
80%
Diferencia de valor de
160 millones
80 millones
60
0
-80 millones
-160 millones
40
20
0
−200
0
200
Diferencia de ELO
En la Eurocopa, todos los partidos se consideran neutrales salvo los que juega Alemania, la anfitriona. Los alemanes tienen un doble beneficio: les damos la ventaja que tiene un equipo cuando juega en casa —en un partido de liga o de clasificación para un mundial, por ejemplo—, pero además le sumamos un empuje extra equivalente a 0,2 goles por partido. Hemos elegido ese número tomando como referencia un análisis de FiveThirtyEight, que ha estimado la ventaja histórica del organizador en un Mundial en 0,4 goles por partido sobre lo esperado.
¿Por qué usamos un modelo que predice goles y no directamente victorias? Tiene dos ventajas hacerlo así: nos sirve para resolver la fase de grupos y para predecir prórrogas (como partidos de 30 minutos). Algunos estudios Dixon & Coles, 1997 dicen que los modelos que predicen goles infraestiman los empates. Hemos comprobado que es así en la Champions, y en las grandes ligas europeas, pero el efecto es menor en los Mundiales, y hemos decidido no hacer ese ajuste con la Eurocopa.
Qué acierto podemos esperar del modelo. Para calibrarlo, hemos usado una base de datos de 18.000 partidos de selecciones desde 2004, incluidos cientos de encuentros de Mundiales y Eurocopas.
Con datos de entrenamiento, el modelo acierta el resultado del 60% de los partidos con equipo local y el 56% en campo neutral. Evaluado en términos probabilísticos, las predicciones del modelo obtienen una puntuación de entre 0,176 y 0,186 (expresado con un Ranking Probability Score, como se explica aquí o aquí. Una precisión razonable, si la comparamos con otros modelos o con las apuestas.

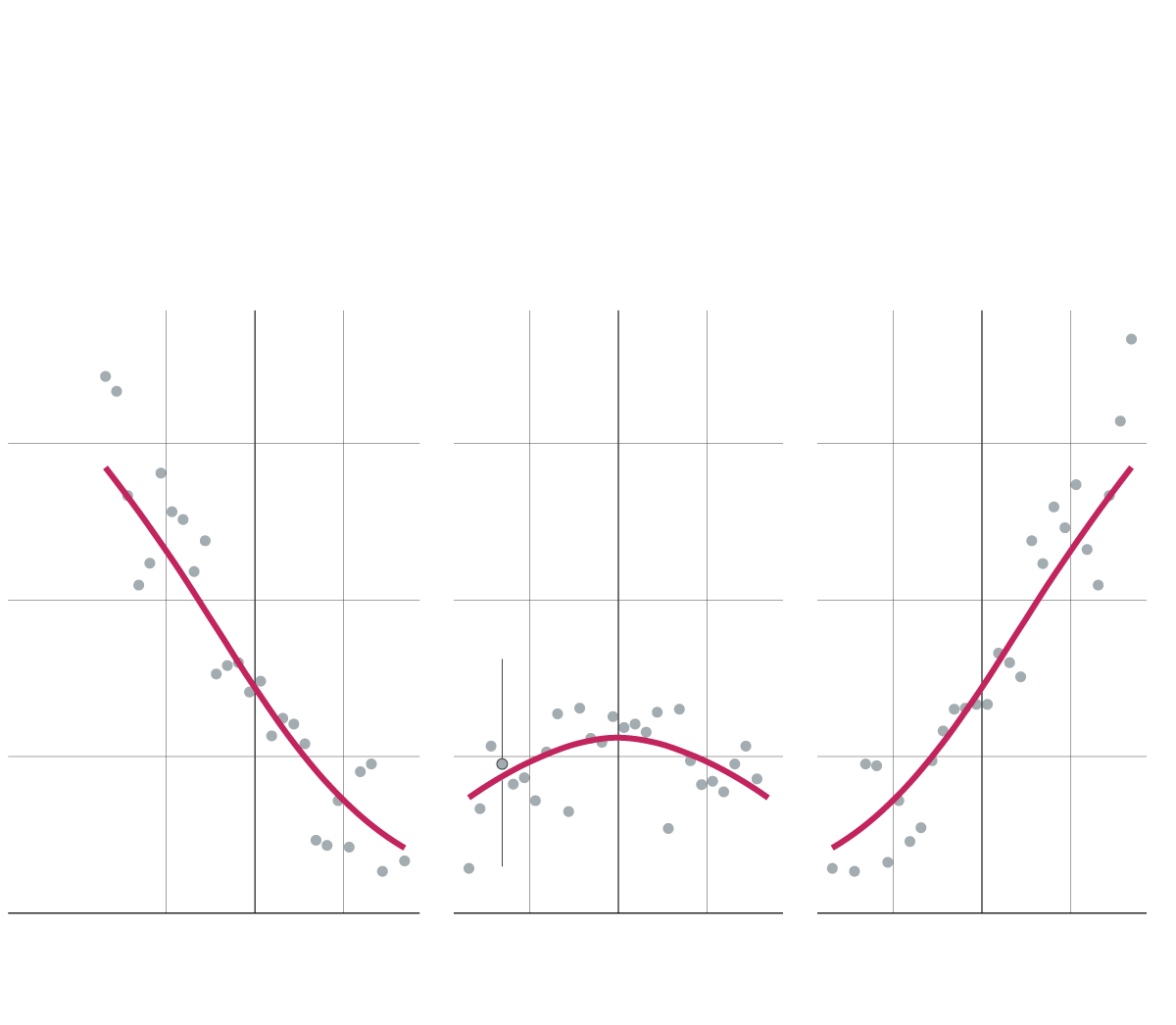
Entrenamiento del modelo. Los puntos representan los resultados de partidos reales y las líneas las predicciones del modelo. Para partidos entre equipos con cierta diferencia de 'ranking' Elo (eje x), se muestra la probabilidad o el porcentaje que acaban en derrota, empate o victoria (eje y).
Derrotas
(prob. en %)
Empates
(prob. en %)
Victorias
(prob. en %)
75%
50
Realidad
25
Modelo
0
−200
0
200
−200
0
200
−200
0
200
Diferencia de ELO
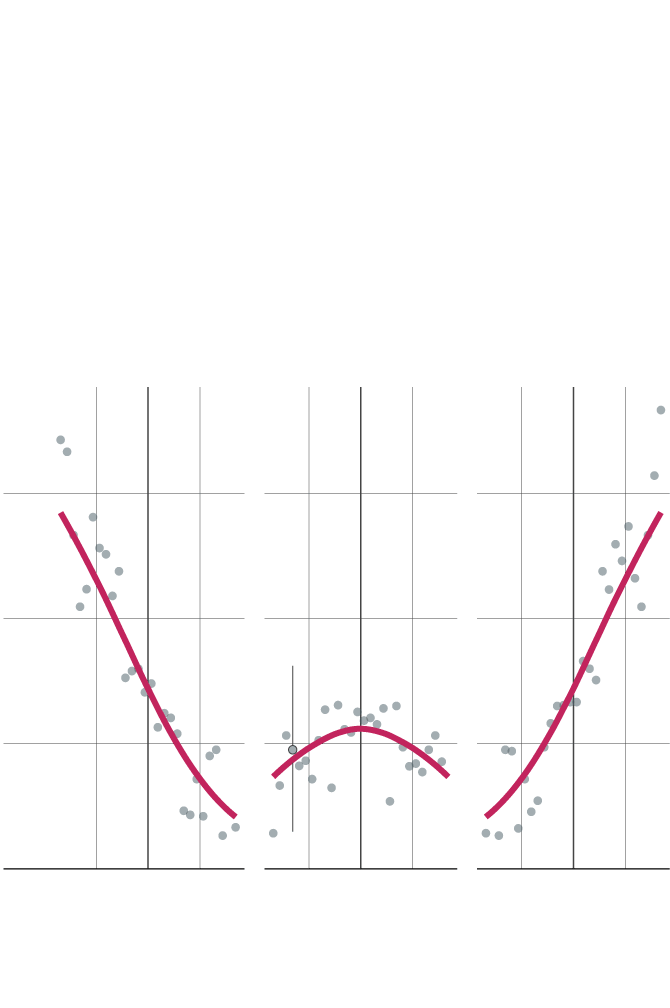
Entrenamiento del modelo. Los puntos representan los resultados de partidos reales y las líneas las predicciones del modelo. Para partidos entre equipos con cierta diferencia de ranking Elo (eje x), se muestra la probabilidad o el porcentaje que acaban en derrota, empate o victoria (eje y).
Derrotas
(prob. en %)
Empates
(prob. en %)
Victorias
(prob. en %)
75%
50
Realidad
25
Modelo
0
−200
0
200
−200
0
200
−200
0
200
Diferencia de ELO
Entrenamiento del modelo. Los puntos representan los resultados de partidos reales y las líneas las predicciones del modelo. Para partidos entre equipos con cierta diferencia de ranking Elo (eje x), se muestra la probabilidad o el porcentaje que acaban en derrota, empate o victoria (eje y).
Derrotas
(prob. en %)
Empates
(prob. en %)
Victorias
(prob. en %)
75%
50
Realidad
25
Modelo
0
−200
0
200
−200
0
200
−200
0
200
Diferencia de ELO
También podéis ver la evaluación que hicimos de nuestro modelo de 2018 y en 2022, tras cada mundial.
Puedes seguir a EL PAÍS Deportes en Facebook y X, o apuntarte aquí para recibir nuestra newsletter semanal.